



suivant: 3.1.3.1.1 Etats quasi-périodiques
monter: 3.1.3 Cas de l'expérience
précédent: 3.1.3 Cas de l'expérience
Table des matières
Figure:
Cliché ombroscopique typique de la cellule rectangulaire.
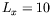 mm,
mm, 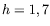 mm,
mm,
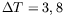 K.
La ligne d'acquisition est représentée en pointillés (- - -).
K.
La ligne d'acquisition est représentée en pointillés (- - -).
|
|
Figure:
Profils d'amplitude dans la cellule rectangulaire pour 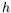 =1,7 mm,
=1,7 mm,
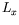 =10 mm,
=10 mm, 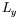 =180 mm. Au seuil (
=180 mm. Au seuil (
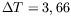 K,
K,
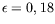 , à gauche en haut), les deux ondes ont sensiblement la
même amplitude et la structure est symétrique. Lorsque l'on
s'éloigne du seuil, l'une des deux ondes gagne sur l'autre
(
, à gauche en haut), les deux ondes ont sensiblement la
même amplitude et la structure est symétrique. Lorsque l'on
s'éloigne du seuil, l'une des deux ondes gagne sur l'autre
(
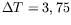 K,
K,
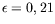 , à gauche en bas).
A droite sont représentés les profils de l'onde dominante exclusivement,
pour différentes valeurs de
, à gauche en bas).
A droite sont représentés les profils de l'onde dominante exclusivement,
pour différentes valeurs de  (3,66 K, 3,75 K, 4,20 K et 4,75 K).
(3,66 K, 3,75 K, 4,20 K et 4,75 K).
|
|
Décrivons en détail l'enveloppe des ondes au seuil et légèrement
au dessus. Un cliché typique est reproduit sur la
figure ![[*]](crossref.png) . La figure
. La figure ![[*]](crossref.png) représente les profils d'amplitude
représente les profils d'amplitude  et
et  de l'onde droite et de
l'onde gauche obtenus après transformée de Hilbert en temps et
filtrage en espace pour séparer les deux sens de propagation. Ce
dernier filtrage a été choisi de sorte à laisser passer le plus
grand nombre de modes possibles et il ne coupe en fait que les très
basses valeurs du nombre d'onde (
de l'onde droite et de
l'onde gauche obtenus après transformée de Hilbert en temps et
filtrage en espace pour séparer les deux sens de propagation. Ce
dernier filtrage a été choisi de sorte à laisser passer le plus
grand nombre de modes possibles et il ne coupe en fait que les très
basses valeurs du nombre d'onde (
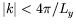 ) et les très hautes
(
) et les très hautes
(
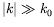 ). Par un souci de clarté, l'onde dominante est
présentée comme une onde droite d'amplitude
). Par un souci de clarté, l'onde dominante est
présentée comme une onde droite d'amplitude 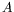 , mais le cas inverse
est équiprobable. Les ondes n'ont pas une amplitude homogène dans la
cellule, mais ont une structure spatiale bien particulière, telle
que :
, mais le cas inverse
est équiprobable. Les ondes n'ont pas une amplitude homogène dans la
cellule, mais ont une structure spatiale bien particulière, telle
que :
- l'amplitude s'annule (ou presque) aux bords en
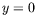 et
et 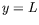 .
.
- les deux ondes co-existent : dans un voisinage de chacun des bords,
l'amplitude de l'onde droite (resp. gauche) est suffisamment faible
pour que l'onde gauche (resp. droite) ne soit pas non-linéairement
« tuée » et donc existe.
- un bord est ainsi source d'onde droite et puits d'onde gauche ;
l'autre bord joue le rôle inverse.
- en aval de son bord source, l'amplitude d'une onde croît
exponentiellement (zone I). Cette zone est mise en évidence
sur la figure
![[*]](crossref.png) .
.
- en aval de cette zone de croissance exponentielle, l'onde atteint
un plateau d'amplitude qui correspond à la saturation non-linéaire
(zone II).
- encore plus en aval, juste avant le bord « puits », l'amplitude de l'onde
atteint une valeur maximale, plus forte que la valeur à saturation
de la zone II. Nous appellerons cette zone le mode de bord (zone III).
Figure:
Profils d'amplitude de la figure ![[*]](crossref.png) -droite,
en échelle logarithmique : les zones de dépendance exponentielle de
l'amplitude sont ainsi mises en valeur. Outre la source étendue, le puit
d'onde (en aval, à droite), présente aussi une zone (de décroissance)
exponentielle, très courte. Il en est de même légèrement en
amont (à gauche) du maximum, dans la partie « montante » du mode
de bord.
-droite,
en échelle logarithmique : les zones de dépendance exponentielle de
l'amplitude sont ainsi mises en valeur. Outre la source étendue, le puit
d'onde (en aval, à droite), présente aussi une zone (de décroissance)
exponentielle, très courte. Il en est de même légèrement en
amont (à gauche) du maximum, dans la partie « montante » du mode
de bord.
|
|
Sous-sections




suivant: 3.1.3.1.1 Etats quasi-périodiques
monter: 3.1.3 Cas de l'expérience
précédent: 3.1.3 Cas de l'expérience
Table des matières
Nicolas Garnier - Thèse de doctorat
![\includegraphics[width=12cm]{ph-rect}](img726.png)
![\includegraphics[width=12cm]{ph-rect}](img726.png)
![\includegraphics[width=8cm]{pr366375}](img728.png)
![\includegraphics[width=8cm]{source5}](img729.png)
![[*]](crossref.png) . La figure
. La figure ![[*]](crossref.png) représente les profils d'amplitude
représente les profils d'amplitude ![]() et
et ![]() de l'onde droite et de
l'onde gauche obtenus après transformée de Hilbert en temps et
filtrage en espace pour séparer les deux sens de propagation. Ce
dernier filtrage a été choisi de sorte à laisser passer le plus
grand nombre de modes possibles et il ne coupe en fait que les très
basses valeurs du nombre d'onde (
de l'onde droite et de
l'onde gauche obtenus après transformée de Hilbert en temps et
filtrage en espace pour séparer les deux sens de propagation. Ce
dernier filtrage a été choisi de sorte à laisser passer le plus
grand nombre de modes possibles et il ne coupe en fait que les très
basses valeurs du nombre d'onde (
![]() ) et les très hautes
(
) et les très hautes
(
![]() ). Par un souci de clarté, l'onde dominante est
présentée comme une onde droite d'amplitude
). Par un souci de clarté, l'onde dominante est
présentée comme une onde droite d'amplitude ![]() , mais le cas inverse
est équiprobable. Les ondes n'ont pas une amplitude homogène dans la
cellule, mais ont une structure spatiale bien particulière, telle
que :
, mais le cas inverse
est équiprobable. Les ondes n'ont pas une amplitude homogène dans la
cellule, mais ont une structure spatiale bien particulière, telle
que :
![[*]](crossref.png) .
.