



suivant: 3.1.3.2.3 Amplitude maximale
monter: 3.1.3.2 b. Recherche de
précédent: 3.1.3.2.1 Amplitude à saturation
Table des matières
Il est aisé de calculer la valeur moyenne
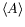 de l'amplitude en
intégrant l'aire située sous le profil d'amplitude locale. Ainsi :
Cette amplitude moyenne joue plus ou moins le rôle de
l'amplitude à saturation pour les plus grandes valeurs de
de l'amplitude en
intégrant l'aire située sous le profil d'amplitude locale. Ainsi :
Cette amplitude moyenne joue plus ou moins le rôle de
l'amplitude à saturation pour les plus grandes valeurs de  ,
mais au contraire de l'amplitude à saturation, elle peut être
définie près du seuil d'apparition des ondes, dans les régimes
où la zone II n'est pas définie.
,
mais au contraire de l'amplitude à saturation, elle peut être
définie près du seuil d'apparition des ondes, dans les régimes
où la zone II n'est pas définie.
Figure:
Evolution de l'amplitude à saturation
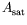 (à gauche)
et de l'amplitude moyenne
(à gauche)
et de l'amplitude moyenne
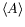 (à droite) dans le rectangle
en fonction de
(à droite) dans le rectangle
en fonction de  .
.
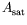 n'a pas un comportement critique clair.
Noter la petite discontinuité de
n'a pas un comportement critique clair.
Noter la petite discontinuité de
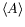 au seuil.
Sur chaque graphe, la droite verticale représente le seuil
expérimental observé à l'il et déduit de l'évolution
de l'amplitude maximale (fig.
au seuil.
Sur chaque graphe, la droite verticale représente le seuil
expérimental observé à l'il et déduit de l'évolution
de l'amplitude maximale (fig. ![[*]](crossref.png) ).
).
![\begin{picture}(0,0)(0,0)
\put(122,85){\makebox(0,0)[l]{\includegraphics[width=3.5cm]{asat2-02}}}
\end{picture}](img746.png) |
Le comportement de l'amplitude moyenne est reproduit sur la
figure ![[*]](crossref.png) . Nous y notons une tendance linéaire qui, si
nous l'extrapolons, nous donne une valeur par défaut du seuil des
ondes : l'amplitude moyenne ne varie pas continuement au seuil. Le
comportement de
. Nous y notons une tendance linéaire qui, si
nous l'extrapolons, nous donne une valeur par défaut du seuil des
ondes : l'amplitude moyenne ne varie pas continuement au seuil. Le
comportement de
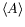 ne peut être expliqué a priori sans une
description de l'enveloppe spatiale de l'onde.
ne peut être expliqué a priori sans une
description de l'enveloppe spatiale de l'onde.




suivant: 3.1.3.2.3 Amplitude maximale
monter: 3.1.3.2 b. Recherche de
précédent: 3.1.3.2.1 Amplitude à saturation
Table des matières
Nicolas Garnier - Thèse de doctorat
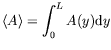
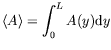
![[*]](crossref.png) . Nous y notons une tendance linéaire qui, si
nous l'extrapolons, nous donne une valeur par défaut du seuil des
ondes : l'amplitude moyenne ne varie pas continuement au seuil. Le
comportement de
. Nous y notons une tendance linéaire qui, si
nous l'extrapolons, nous donne une valeur par défaut du seuil des
ondes : l'amplitude moyenne ne varie pas continuement au seuil. Le
comportement de
![]() ne peut être expliqué a priori sans une
description de l'enveloppe spatiale de l'onde.
ne peut être expliqué a priori sans une
description de l'enveloppe spatiale de l'onde.