



suivant: 1.1.2.0.2 Effets thermogravitaires
monter: 1.1.2 Réduction de la
précédent: 1.1.2 Réduction de la
Table des matières
Nous étudions un fluide en mouvement et un champ de température
associé. Nous avons donc deux grandeurs de dimension
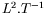 traduisant respectivement la diffusion de la vitesse et celle de la
température : la viscosité cinématique
traduisant respectivement la diffusion de la vitesse et celle de la
température : la viscosité cinématique 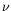 et la diffusivité
thermique
et la diffusivité
thermique 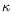 . Leur rapport est appellé nombre de Prandtl :
Il caractérise l'importance relative des effets thermiques et
visqueux. Si l'on imagine par exemple un élément de fluide de taille
caractérique
. Leur rapport est appellé nombre de Prandtl :
Il caractérise l'importance relative des effets thermiques et
visqueux. Si l'on imagine par exemple un élément de fluide de taille
caractérique 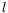 , les temps de diffusion visqueuse
, les temps de diffusion visqueuse 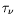 et de la
chaleur
et de la
chaleur
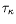 seront donnés par :
On note ainsi que pour les fluides de grand nombre de Prandtl (huiles
silicones très visqueuses par exemple), le temps thermique est plus
grand que le temps visqueux et que les processus de diffusion de la
chaleur pilotent le mouvement du fluide. Pour les faibles valeurs du
nombre de Prandtl (métaux liquides par exemple), les effets thermiques
s'amenuisent et le comportement du fluide est essentiellement
hydrodynamique. Nos expériences sont réalisées avec un liquide de
nombre de Prandtl égal à 10.
seront donnés par :
On note ainsi que pour les fluides de grand nombre de Prandtl (huiles
silicones très visqueuses par exemple), le temps thermique est plus
grand que le temps visqueux et que les processus de diffusion de la
chaleur pilotent le mouvement du fluide. Pour les faibles valeurs du
nombre de Prandtl (métaux liquides par exemple), les effets thermiques
s'amenuisent et le comportement du fluide est essentiellement
hydrodynamique. Nos expériences sont réalisées avec un liquide de
nombre de Prandtl égal à 10.




suivant: 1.1.2.0.2 Effets thermogravitaires
monter: 1.1.2 Réduction de la
précédent: 1.1.2 Réduction de la
Table des matières
Nicolas Garnier - Thèse de doctorat