



suivant: 1.1.2.0.3 Effets thermocapillaires
monter: 1.1.2 Réduction de la
précédent: 1.1.2.0.1 Description du fluide
Table des matières
La poussée d'Archimède due à un gradient thermique
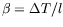 -- une différence de température
-- une différence de température  appliquée sur
une échelle
appliquée sur
une échelle 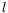 -- imposé à une couche de fluide de hauteur
-- imposé à une couche de fluide de hauteur 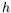 peut être comparée aux forces dissipatives apparaissant dans
l'équation de Navier-Stokes (éq.
peut être comparée aux forces dissipatives apparaissant dans
l'équation de Navier-Stokes (éq. ![[*]](crossref.png) ). Celles-ci sont
dues à l'existence d'une viscosité
). Celles-ci sont
dues à l'existence d'une viscosité 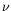 et d'une diffusivité
et d'une diffusivité
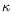 finies. Le rapport résultant est appellé nombre de
Rayleigh :
Un grand nombre de Rayleigh exprime le fait que la vitesse d'ascension
d'une particule fluide sous l'effet de la poussée d'Archimède est
telle que la diffusion thermique n'a pas le temps d'agir :
finies. Le rapport résultant est appellé nombre de
Rayleigh :
Un grand nombre de Rayleigh exprime le fait que la vitesse d'ascension
d'une particule fluide sous l'effet de la poussée d'Archimède est
telle que la diffusion thermique n'a pas le temps d'agir :
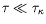 . Dans le cas où la contrainte thermique est appliquée
verticalement (cas de Rayleigh-Bénard), on a
. Dans le cas où la contrainte thermique est appliquée
verticalement (cas de Rayleigh-Bénard), on a 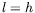 et une
simplification de l'expression ci-dessus. Dans le cas où elle est
appliquée horizontalement, on a
et une
simplification de l'expression ci-dessus. Dans le cas où elle est
appliquée horizontalement, on a
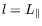 , la taille de la
cellule dans la direction du gradient.
, la taille de la
cellule dans la direction du gradient.
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ). Celles-ci sont
dues à l'existence d'une viscosité
). Celles-ci sont
dues à l'existence d'une viscosité