



suivant: 1.2.1.2 Conditions aux limites
monter: 1.2.1 Equations de Boussinesq
précédent: 1.2.1 Equations de Boussinesq
Table des matières
Si l'on tient compte des effets thermogravitaires, le système
d'équations décrivant l'évolution de la vitesse
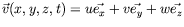 , de la température
, de la température
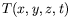 et de la pression
et de la pression
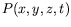 du fluide est constitué
par les équations de Navier-Stokes, de conservation de la masse et de
l'énergie prises dans l'approximation de Boussinesq :
du fluide est constitué
par les équations de Navier-Stokes, de conservation de la masse et de
l'énergie prises dans l'approximation de Boussinesq :
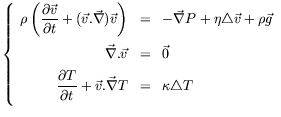 |
(1.6) |
La masse volumique est exprimée par la formule (![[*]](crossref.png) ).
L'approximation de Boussinesq consiste à négliger les variations de
).
L'approximation de Boussinesq consiste à négliger les variations de
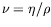 et
et 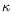 , tout en ne faisant dépendre
, tout en ne faisant dépendre 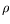 que de
que de
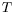 et uniquement pour le terme de gravité.
et uniquement pour le terme de gravité.
Nicolas Garnier - Thèse de doctorat
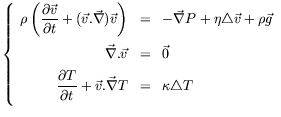
![[*]](crossref.png) ).
L'approximation de Boussinesq consiste à négliger les variations de
).
L'approximation de Boussinesq consiste à négliger les variations de
![]() et
et ![]() , tout en ne faisant dépendre
, tout en ne faisant dépendre ![]() que de
que de
![]() et uniquement pour le terme de gravité.
et uniquement pour le terme de gravité.