



suivant: 1.1.1.2 Effet thermocapillaire
monter: 1.1.1 Mécanismes thermogravitaire et
précédent: 1.1.1 Mécanismes thermogravitaire et
Table des matières
Le premier mécanisme susceptible d'engendrer un mouvement dans la
couche de fluide est la variation de la densité 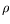 du fluide avec
la température, que nous modélisons par l'équation d'état
suivante :
du fluide avec
la température, que nous modélisons par l'équation d'état
suivante :
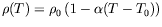 |
(1.1) |
où
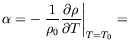
cste

Pour des raisons de stabilité thermodynamique, on a généralement
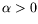 dans les fluides purs. Cette dépendance de
dans les fluides purs. Cette dépendance de 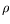 avec la
température est à l'origine de la convection de Rayleigh-Bénard
lorsqu'existe un gradient vertical négatif de température. Dans
notre cas, elle induit une dilatation du fluide du côté chaud, donc
une élévation de la surface, et ainsi une différence de pression
horizontale à une hauteur d'observation fixée (cf
Fig.
avec la
température est à l'origine de la convection de Rayleigh-Bénard
lorsqu'existe un gradient vertical négatif de température. Dans
notre cas, elle induit une dilatation du fluide du côté chaud, donc
une élévation de la surface, et ainsi une différence de pression
horizontale à une hauteur d'observation fixée (cf
Fig. ![[*]](crossref.png) ). En surface, le fluide est donc animé d'un
mouvement de la zone chaude vers la zone froide.
). En surface, le fluide est donc animé d'un
mouvement de la zone chaude vers la zone froide.
Figure:
Déformation élémentaire de la surface libre par la poussée d'Archimède
due à un gradient horizontal de température.
![\begin{figure}
\begin{center}
\begin{picture}(120,100)(0,0)
\linethickness{1p...
...){\makebox(0,0)[b]{$\vec{\nabla}T$}}
\end{picture}
\end{center}
\end{figure}](img19.png) |
Ce mécanisme opère en volume, et il est présent dès que la
différence de température  est non nulle. On s'attend par
ailleurs à ce qu'il soit d'autant plus important que la hauteur de
fluide est plus grande.
est non nulle. On s'attend par
ailleurs à ce qu'il soit d'autant plus important que la hauteur de
fluide est plus grande.
En coordonnées cartésiennes, avec
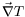 selon
selon
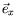 , il est possible de calculer la variation de la hauteur
survenant sur un petit élément de surface
, il est possible de calculer la variation de la hauteur
survenant sur un petit élément de surface
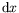 lors de
l'imposition d'un gradient
lors de
l'imposition d'un gradient
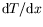 ; nous obtenons (les calculs
sont reportés en annexe
; nous obtenons (les calculs
sont reportés en annexe ![[*]](crossref.png) ,
page
,
page ![[*]](crossref.png) ) :
) :
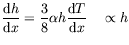 |
(1.2) |
Application numérique: avec
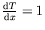 K/cm, et
K/cm, et
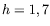 mm, il vient
mm, il vient
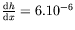 pour l'eau et
pour l'eau et
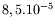 pour l'huile aux silicones que nous utilisons, ce qui est
tout à fait négligeable dans nos réalisations expérimentales.
pour l'huile aux silicones que nous utilisons, ce qui est
tout à fait négligeable dans nos réalisations expérimentales.




suivant: 1.1.1.2 Effet thermocapillaire
monter: 1.1.1 Mécanismes thermogravitaire et
précédent: 1.1.1 Mécanismes thermogravitaire et
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ). En surface, le fluide est donc animé d'un
mouvement de la zone chaude vers la zone froide.
). En surface, le fluide est donc animé d'un
mouvement de la zone chaude vers la zone froide.
![\begin{figure}
\begin{center}
\begin{picture}(120,100)(0,0)
\linethickness{1p...
...){\makebox(0,0)[b]{$\vec{\nabla}T$}}
\end{picture}
\end{center}
\end{figure}](img19.png)
![]() est non nulle. On s'attend par
ailleurs à ce qu'il soit d'autant plus important que la hauteur de
fluide est plus grande.
est non nulle. On s'attend par
ailleurs à ce qu'il soit d'autant plus important que la hauteur de
fluide est plus grande.
![]() selon
selon
![]() , il est possible de calculer la variation de la hauteur
survenant sur un petit élément de surface
, il est possible de calculer la variation de la hauteur
survenant sur un petit élément de surface
![]() lors de
l'imposition d'un gradient
lors de
l'imposition d'un gradient
![]() ; nous obtenons (les calculs
sont reportés en annexe
; nous obtenons (les calculs
sont reportés en annexe ![[*]](crossref.png) ,
page
,
page ![[*]](crossref.png) ) :
) :