![[*]](crossref.png) ) et (
) et (![[*]](crossref.png) ) qui
décrivent de combien s'élève la surface libre d'un fluide soumis
à un gradient horizontal de température
) qui
décrivent de combien s'élève la surface libre d'un fluide soumis
à un gradient horizontal de température
Nous allons ici détailler comment sont obtenues les
formules (![[*]](crossref.png) ) et (
) et (![[*]](crossref.png) ) qui
décrivent de combien s'élève la surface libre d'un fluide soumis
à un gradient horizontal de température
) qui
décrivent de combien s'élève la surface libre d'un fluide soumis
à un gradient horizontal de température
![]() par l'effet de la thermogravité et de la thermocapillarité. Les
calculs ci-dessous sont inspirés du calcul présenté
par Guyon et al. (1991).
par l'effet de la thermogravité et de la thermocapillarité. Les
calculs ci-dessous sont inspirés du calcul présenté
par Guyon et al. (1991).
![\includegraphics[width=4cm]{meca-dx}](img1173.png)
![\begin{picture}(0,0)(-205,-32)
\put(-15, -3){\makebox(0,0)[l]{$x$}}
\put( 46, ...
...box(0,0)[r]{$T$}}
\put( 65, 35){\makebox(0,0)[l]{$T+\mathrm dT$}}
\end{picture}](img1174.png)
Nous considérons un volume de fluide de hauteur ![]() compris entre
compris entre
![]() et
et
![]() en nous restreignant au plan
en nous restreignant au plan ![]() . Nous supposons
que la vitesse peut être mise sous la forme :
. Nous supposons
que la vitesse peut être mise sous la forme :
![]() , i.e., que la vitesse verticale est négligeable (elle
est d'ailleurs nulle en géométrie rectangulaire). L'équation de
Navier-Stokes en régime stationnaire se réduit à :
, i.e., que la vitesse verticale est négligeable (elle
est d'ailleurs nulle en géométrie rectangulaire). L'équation de
Navier-Stokes en régime stationnaire se réduit à :
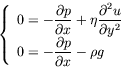
avec :
Nous fixons les constantes d'intégration avec les conditions suivantes :
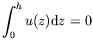 |
|
où ![]() est la pression atmosphérique. Nous linéarisons
la dépendance de
est la pression atmosphérique. Nous linéarisons
la dépendance de ![]() en
en ![]() et nous en déduisons alors :
et nous en déduisons alors :
d'où :
Nous relions ensuite cette expression à la tension de surface grâce à la condition aux limites cinématique tangentielle à la surface :
d'où, en négligeant
![]() devant
devant ![]() :
:
| (A.1) |
Nous en déduisons les formules (![[*]](crossref.png) )
et (
)
et (![[*]](crossref.png) ) donnant la déflection de surface dans le
cas purement thermogravitaire (
) donnant la déflection de surface dans le
cas purement thermogravitaire (![]() ) et dans le cas purement
thermocapillaire (
) et dans le cas purement
thermocapillaire (![]() ).
).
La variation de surface d'origine thermogravitaire varie
proportionnellement à ![]() alors que la variation de surface d'origine
thermocapillaire varie comme l'inverse de
alors que la variation de surface d'origine
thermocapillaire varie comme l'inverse de ![]() . Pour des très faibles
valeurs de la hauteur (
. Pour des très faibles
valeurs de la hauteur (![]() mm), nous avons expérimentalement
constaté dans la cellule « LOTUS » une déflection de la hauteur
atteignant déjà 50% de la valeur nominale au seuil des ondes OH2...
mm), nous avons expérimentalement
constaté dans la cellule « LOTUS » une déflection de la hauteur
atteignant déjà 50% de la valeur nominale au seuil des ondes OH2...