



suivant: 1.1.1.3 Commentaires
monter: 1.1.1 Mécanismes thermogravitaire et
précédent: 1.1.1.1 Effet thermogravitaire
Table des matières
1.1.1.2 Effet thermocapillaire
Le second -- et principal dans notre cas -- mécanisme engendrant
l'écoulement de base est dû à la variation de la tension de
surface 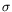 avec la température :
où
avec la température :
où
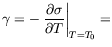
cste

Pour la plupart des fluides, la tension de surface est reliée aux
forces de Van der Waals ; une augmentation de l'agitation thermique
réduit l'influence de ces interactions et diminue la valeur de la
tension de surface. On en déduit que
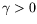 , ce qui est
vérifié pour la plupart des fluides. Une différence de
température en surface se traduit par une différence de tension de
surface, ce qui meut le fluide en surface de la zone chaude (
, ce qui est
vérifié pour la plupart des fluides. Une différence de
température en surface se traduit par une différence de tension de
surface, ce qui meut le fluide en surface de la zone chaude (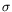 faible) vers la zone froide (
faible) vers la zone froide (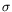 fort) (cf
Fig.
fort) (cf
Fig. ![[*]](crossref.png) ). Le fluide étant visqueux, ce mouvement
diffuse dans le volume sous la surface. Par conservation de la matière
à travers une section verticale quelconque, le bas de la couche de
fluide doit alors être animé d'une vitesse de sens opposé, ce qui
traduit sa recirculation et l'existence d'un rouleau dans l'écoulement
de base.
). Le fluide étant visqueux, ce mouvement
diffuse dans le volume sous la surface. Par conservation de la matière
à travers une section verticale quelconque, le bas de la couche de
fluide doit alors être animé d'une vitesse de sens opposé, ce qui
traduit sa recirculation et l'existence d'un rouleau dans l'écoulement
de base.
Figure:
Déformation élémentaire de la surface libre par une différence
de tension de surface due à un gradient horizontal de température.
![\begin{figure}
\begin{center}
\begin{picture}(120,100)(0,0)
\linethickness{1p...
...){\makebox(0,0)[b]{$\vec{\nabla}T$}}
\end{picture}
\end{center}
\end{figure}](img19.png) |
Ce mécanisme opère en surface, mais diffuse dans le volume et sera
lui aussi présent dès que
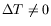 .
.
En coordonnées cartésiennes, avec
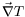 selon
selon
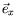 , la variation de hauteur s'écrit
(annexe
, la variation de hauteur s'écrit
(annexe ![[*]](crossref.png) ou Guyon et al. (1991)) :
ou Guyon et al. (1991)) :
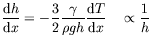 |
(1.3) |
Application numérique : avec
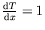 K/cm et
K/cm et
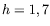 mm, il vient
mm, il vient
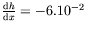 pour l'eau et
seulement
pour l'eau et
seulement
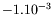 pour l'huile aux silicones que nous utilisons, ce
qui est un effet très petit dans nos expériences.
pour l'huile aux silicones que nous utilisons, ce
qui est un effet très petit dans nos expériences.




suivant: 1.1.1.3 Commentaires
monter: 1.1.1 Mécanismes thermogravitaire et
précédent: 1.1.1.1 Effet thermogravitaire
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ). Le fluide étant visqueux, ce mouvement
diffuse dans le volume sous la surface. Par conservation de la matière
à travers une section verticale quelconque, le bas de la couche de
fluide doit alors être animé d'une vitesse de sens opposé, ce qui
traduit sa recirculation et l'existence d'un rouleau dans l'écoulement
de base.
). Le fluide étant visqueux, ce mouvement
diffuse dans le volume sous la surface. Par conservation de la matière
à travers une section verticale quelconque, le bas de la couche de
fluide doit alors être animé d'une vitesse de sens opposé, ce qui
traduit sa recirculation et l'existence d'un rouleau dans l'écoulement
de base.
![\begin{figure}
\begin{center}
\begin{picture}(120,100)(0,0)
\linethickness{1p...
...){\makebox(0,0)[b]{$\vec{\nabla}T$}}
\end{picture}
\end{center}
\end{figure}](img19.png)
![]() .
.
![]() selon
selon
![]() , la variation de hauteur s'écrit
(annexe
, la variation de hauteur s'écrit
(annexe ![[*]](crossref.png) ou Guyon et al. (1991)) :
ou Guyon et al. (1991)) :