



suivant: 1.2.1.1 Equations en volume
monter: 1.2 Calcul de l'écoulement
précédent: 1.2 Calcul de l'écoulement
Table des matières
Pour déterminer la forme de l'écoulement de base, nous résolvons
les équations de Navier-Stokes associées aux conditions limites
adéquates. Nous considérons une couche de fluide de hauteur 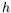 ,
avec sa surface supérieure libre. Cette couche est soumise à un
gradient horizontal de température
,
avec sa surface supérieure libre. Cette couche est soumise à un
gradient horizontal de température
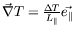 qui définit la direction
qui définit la direction
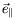 . La direction verticale est notée
. La direction verticale est notée 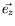 .
Encore une fois, nous invoquons le principe de Curie pour ne garder que
ces deux directions d'espace pertinentes.
Dans le cas rectangulaire, nous aurons
.
Encore une fois, nous invoquons le principe de Curie pour ne garder que
ces deux directions d'espace pertinentes.
Dans le cas rectangulaire, nous aurons
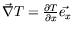 , donc
, donc
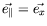 (et
(et
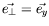 ). Dans le cas cylindrique, nous aurons de
même
). Dans le cas cylindrique, nous aurons de
même
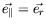 (et
(et
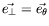 ).
Il nous arrivera parfois de noter
).
Il nous arrivera parfois de noter  (resp.
(resp. 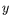 ) la variable d'espace
dans la direction horizontale du gradient (resp. perpendiculaire au
gradient) tout en restant dans le cas général (cartésien ou
cylindrique).
) la variable d'espace
dans la direction horizontale du gradient (resp. perpendiculaire au
gradient) tout en restant dans le cas général (cartésien ou
cylindrique).
Sous-sections
Nicolas Garnier - Thèse de doctorat