



suivant: 1.2.1 Equations de Boussinesq
monter: 1. Les ondes hydrothermales
précédent: 1.1.2.0.8 Rapports d'aspect
Table des matières
1.2 Calcul de l'écoulement de base
Nous allons présenter ici les formulations de l'écoulement de base
thermocapillaire et thermogravitaire dans les géométries
rectangulaire et cylindrique. Une revue des phénomènes
abordés a été produite par Davis (1987). Les résultats
concernant l'écoulement de base purement thermocapillaire en
coordonnées cartésiennes ont été décrits en détail par
Sen et Davis (1982) et utilisés par Smith et Davis (1983a) ; l'écoulement
tenant en plus compte de la gravité (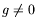 ) peut être trouvé
par exemple dans les travaux de Laure et al. (1990), Mercier et Normand (1996),
Mercier (1997). Nous retrouvons ici ces résultats grâce à une
méthode perturbative équivalente à celle introduite par
Laure et al. (1990) dans le cas rectangulaire sans gravité ; nous les
complétons dans le cas général et en géométrie cylindrique.
Les expressions trouvées sont donc celles d'un écoulement en
géométrie infiniment étendue (extensions horizontales infinies).
) peut être trouvé
par exemple dans les travaux de Laure et al. (1990), Mercier et Normand (1996),
Mercier (1997). Nous retrouvons ici ces résultats grâce à une
méthode perturbative équivalente à celle introduite par
Laure et al. (1990) dans le cas rectangulaire sans gravité ; nous les
complétons dans le cas général et en géométrie cylindrique.
Les expressions trouvées sont donc celles d'un écoulement en
géométrie infiniment étendue (extensions horizontales infinies).
Sous-sections
Nicolas Garnier - Thèse de doctorat