



suivant: 1.3 Analyse de stabilité
monter: 1.2 Calcul de l'écoulement
précédent: 1.2.2 Géométrie rectangulaire
Table des matières
1.2.3 Géométrie cylindrique
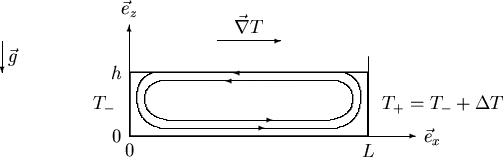
Figure:
Section de la géométrie cylindrique et notations associées.
Par convention, on écrira toujours
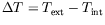 ,
le signe de
,
le signe de 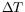 sera donc quelconque.
L'axe des
sera donc quelconque.
L'axe des 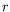 est orienté de l'intérieur vers l'extérieur.
Deux lignes de courant de l'écoulement de base sont symboliquement
représentées sur lesquelles est perceptible une dépendance en
est orienté de l'intérieur vers l'extérieur.
Deux lignes de courant de l'écoulement de base sont symboliquement
représentées sur lesquelles est perceptible une dépendance en 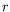 .
.
 |
Si le développement en
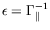 était
presque inutile en géométrie rectangulaire, il s'avère
intéressant dans le cas plus ardu de la géométrie cylindrique où
il a été utilisé par Vrane et Smith (1996). Nous écrivons ici
était
presque inutile en géométrie rectangulaire, il s'avère
intéressant dans le cas plus ardu de la géométrie cylindrique où
il a été utilisé par Vrane et Smith (1996). Nous écrivons ici
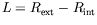 la longueur de la cellule dans le sens
du gradient (figure
la longueur de la cellule dans le sens
du gradient (figure ![[*]](crossref.png) ) et
) et
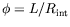 le paramètre de courbure. Nous pouvons alors
écrire la coordonnée spatiale dans le sens du gradient (radial) à
l'aide d'une variable adimensionnée
le paramètre de courbure. Nous pouvons alors
écrire la coordonnée spatiale dans le sens du gradient (radial) à
l'aide d'une variable adimensionnée 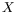 :
:
Là encore, 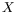 sera la variable lente (variations sur l'échelle
sera la variable lente (variations sur l'échelle  )
par opposition à
)
par opposition à  et
et 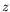 (variations sur l'échelle
(variations sur l'échelle 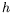 ).
Contrairement au cas rectangulaire, le problème n'est ici plus
symétrique sous la transformation
).
Contrairement au cas rectangulaire, le problème n'est ici plus
symétrique sous la transformation
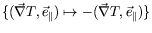 , et nous choisissons de
noter
, et nous choisissons de
noter
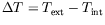 quels que soient les
côtés chaud et froid.
A l'ordre le plus bas en
quels que soient les
côtés chaud et froid.
A l'ordre le plus bas en 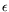 , une résolution du système
analogue au cas rectangulaire conduit à :
où
, une résolution du système
analogue au cas rectangulaire conduit à :
où
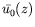 est le même polynôme de degré 3 en
est le même polynôme de degré 3 en 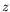 que
dans le cas rectangulaire, ce qui traduit la même allure des profils
verticaux de vitesse
que
dans le cas rectangulaire, ce qui traduit la même allure des profils
verticaux de vitesse 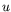 . Le profil conductif
. Le profil conductif
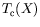 apparaît
encore au premier ordre, mais il s'agit maintenant du profil conductif
en géométrie cylindrique :
La dépendance hyperbolique en
apparaît
encore au premier ordre, mais il s'agit maintenant du profil conductif
en géométrie cylindrique :
La dépendance hyperbolique en 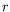 du profil de vitesse en
géométrie cylindrique est traduite par une enveloppe lentement
variable en
du profil de vitesse en
géométrie cylindrique est traduite par une enveloppe lentement
variable en 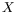 , notée
, notée 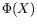 :
Cette enveloppe peut être interprétée comme le flux unitaire de
température à travers la surface extérieure verticale d'un
cylindre de rayon
:
Cette enveloppe peut être interprétée comme le flux unitaire de
température à travers la surface extérieure verticale d'un
cylindre de rayon 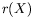 .
.
A l'ordre suivant, il vient :
où 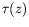 est le même polynôme en
est le même polynôme en 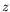 que dans le cas
rectangulaire, et
que dans le cas
rectangulaire, et
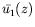 un nouveau polynôme en
un nouveau polynôme en 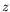 traduisant
le couplage entre
traduisant
le couplage entre 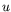 et
et 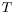 dû à la géométrie cylindrique. Ce
polynôme a, dans le cas général (
dû à la géométrie cylindrique. Ce
polynôme a, dans le cas général (
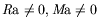 ), une
expression compliquée. Dans le cas purement thermocapillaire (
), une
expression compliquée. Dans le cas purement thermocapillaire (
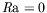 ), et pour un fond conducteur, il s'écrit plus simplement :
Dans le cas d'un fond isolant, l'expression de
), et pour un fond conducteur, il s'écrit plus simplement :
Dans le cas d'un fond isolant, l'expression de 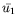 (z) est
déduite de la précédente remplaçant le terme en
(z) est
déduite de la précédente remplaçant le terme en
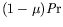 par 1.
par 1.
A l'ordre suivant, on trouve
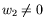 , ce qui traduit l'apparition
d'une vitesse verticale, inexistante dans le cas rectangulaire. De
même, les termes suivants pour
, ce qui traduit l'apparition
d'une vitesse verticale, inexistante dans le cas rectangulaire. De
même, les termes suivants pour 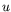 et
et 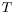 ne seront pas nuls, mais de
plus en plus petits pourvu que
ne seront pas nuls, mais de
plus en plus petits pourvu que
 soit faible. Le
développement en
soit faible. Le
développement en
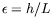 qui donnait parfaitement
l'écoulement de base en géométrie infinie dans le cas
rectangulaire ne donne ici qu'un développement approché car la
géométrie ne peut être que semi-infinie à cause de la
singularité en
qui donnait parfaitement
l'écoulement de base en géométrie infinie dans le cas
rectangulaire ne donne ici qu'un développement approché car la
géométrie ne peut être que semi-infinie à cause de la
singularité en 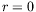 (
(
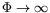 ). Néanmoins, les
résultats obtenus dans le cas rectangulaire peuvent se déduire des
expressions cylindriques par la limite des faibles courbures,
réalisée loin du point singulier
). Néanmoins, les
résultats obtenus dans le cas rectangulaire peuvent se déduire des
expressions cylindriques par la limite des faibles courbures,
réalisée loin du point singulier 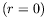 :
:
Le bilan de nos calculs peut être résumé ainsi :
 |
(1.8) |
Nous poserons dans la suite :

et
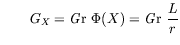
 représente alors un nombre de Grashoff local qui tient compte de
la courbure et
représente alors un nombre de Grashoff local qui tient compte de
la courbure et 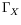 représente les effets de courbure relatifs.
représente les effets de courbure relatifs.




suivant: 1.3 Analyse de stabilité
monter: 1.2 Calcul de l'écoulement
précédent: 1.2.2 Géométrie rectangulaire
Table des matières
Nicolas Garnier - Thèse de doctorat


![]() était
presque inutile en géométrie rectangulaire, il s'avère
intéressant dans le cas plus ardu de la géométrie cylindrique où
il a été utilisé par Vrane et Smith (1996). Nous écrivons ici
était
presque inutile en géométrie rectangulaire, il s'avère
intéressant dans le cas plus ardu de la géométrie cylindrique où
il a été utilisé par Vrane et Smith (1996). Nous écrivons ici
![]() la longueur de la cellule dans le sens
du gradient (figure
la longueur de la cellule dans le sens
du gradient (figure ![[*]](crossref.png) ) et
) et
![]() le paramètre de courbure. Nous pouvons alors
écrire la coordonnée spatiale dans le sens du gradient (radial) à
l'aide d'une variable adimensionnée
le paramètre de courbure. Nous pouvons alors
écrire la coordonnée spatiale dans le sens du gradient (radial) à
l'aide d'une variable adimensionnée ![]() :
:
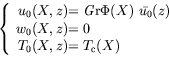

![]() , ce qui traduit l'apparition
d'une vitesse verticale, inexistante dans le cas rectangulaire. De
même, les termes suivants pour
, ce qui traduit l'apparition
d'une vitesse verticale, inexistante dans le cas rectangulaire. De
même, les termes suivants pour ![]() et
et ![]() ne seront pas nuls, mais de
plus en plus petits pourvu que
ne seront pas nuls, mais de
plus en plus petits pourvu que
![]() soit faible. Le
développement en
soit faible. Le
développement en
![]() qui donnait parfaitement
l'écoulement de base en géométrie infinie dans le cas
rectangulaire ne donne ici qu'un développement approché car la
géométrie ne peut être que semi-infinie à cause de la
singularité en
qui donnait parfaitement
l'écoulement de base en géométrie infinie dans le cas
rectangulaire ne donne ici qu'un développement approché car la
géométrie ne peut être que semi-infinie à cause de la
singularité en ![]() (
(
![]() ). Néanmoins, les
résultats obtenus dans le cas rectangulaire peuvent se déduire des
expressions cylindriques par la limite des faibles courbures,
réalisée loin du point singulier
). Néanmoins, les
résultats obtenus dans le cas rectangulaire peuvent se déduire des
expressions cylindriques par la limite des faibles courbures,
réalisée loin du point singulier ![]() :
: