



suivant: 1.2.3 Géométrie cylindrique
monter: 1.2 Calcul de l'écoulement
précédent: 1.2.1.3 Adimensionalisation et petit
Table des matières
1.2.2 Géométrie rectangulaire
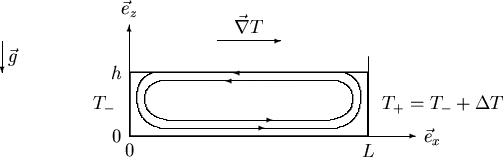
Figure:
Section de la géométrie rectangulaire et notations associées.
L'axe des  est orienté du froid vers le chaud.
Deux lignes de courant de l'écoulement de base sont symboliquement
représentées. Nous avons de plus illustré l'effet des parois en
est orienté du froid vers le chaud.
Deux lignes de courant de l'écoulement de base sont symboliquement
représentées. Nous avons de plus illustré l'effet des parois en
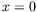 et
et 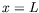 (recirculation du fluide) ; le calcul perturbatif effectué
dans le texte ne donne accès qu'à l'écoulement loin de ces parois.
(recirculation du fluide) ; le calcul perturbatif effectué
dans le texte ne donne accès qu'à l'écoulement loin de ces parois.
 |
Nous considérons que le fluide est dans une boîte finie de
longueur  selon la direction du gradient
(figure
selon la direction du gradient
(figure ![[*]](crossref.png) ) et nous notons l'abscisse
adimensionnée
) et nous notons l'abscisse
adimensionnée
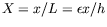 . Ainsi, la variable
. Ainsi, la variable 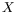 sera
une variable « lente » par rapport à la variable
sera
une variable « lente » par rapport à la variable 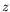 .
.
Nous décrivons précisement la résolution du système à l'ordre
le plus bas en 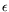 ; la résolution aux ordres suivants
s'effectue de la même façon. A l'ordre 0 en
; la résolution aux ordres suivants
s'effectue de la même façon. A l'ordre 0 en 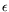 , le
système d'équations s'écrit :
, le
système d'équations s'écrit :
La troisième équation se résoud en utilisant les conditions aux
limites mécaniques en 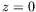 et il vient
et il vient 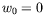 , i.e. pas de vitesse
verticale. La quatrième équation se ré-écrit alors plus
simplement comme l'équation de diffusion de la chaleur à une
dimension (selon
, i.e. pas de vitesse
verticale. La quatrième équation se ré-écrit alors plus
simplement comme l'équation de diffusion de la chaleur à une
dimension (selon 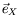 ) ; en utilisant les conditions aux limites
thermiques en
) ; en utilisant les conditions aux limites
thermiques en 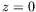 et
et 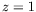 , nous trouvons
, nous trouvons
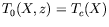 , i.e. le
profil conducteur, indépendant de
, i.e. le
profil conducteur, indépendant de 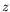 . Nous éliminons ensuite la
pression entre les deux premières équations et nous utilisons les
expressions de
. Nous éliminons ensuite la
pression entre les deux premières équations et nous utilisons les
expressions de 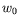 et
et 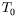 ; il vient :
Nous en déduisons que
; il vient :
Nous en déduisons que 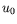 est un polynôme de degré 3 en
est un polynôme de degré 3 en 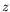 dont
les coefficients sont éventuellement des fonctions de
dont
les coefficients sont éventuellement des fonctions de 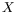 . En
utilisant les conditions aux limites mécaniques et la conservation de
la matière dans une section verticale de la cellule, nous obtenons les
valeurs des coefficients. Dans le cas rectangulaire, ces derniers sont
indépendants de
. En
utilisant les conditions aux limites mécaniques et la conservation de
la matière dans une section verticale de la cellule, nous obtenons les
valeurs des coefficients. Dans le cas rectangulaire, ces derniers sont
indépendants de 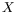 , et il en est donc de même de
, et il en est donc de même de 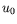 . Nous avons
ainsi :
où
. Nous avons
ainsi :
où
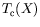 est le profil conductif de température et
est le profil conductif de température et
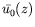 est un polynôme de degré 3 en
est un polynôme de degré 3 en 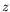 qui traduit la
structure du profil vertical de vitesse :
A l'ordre suivant (ordre
qui traduit la
structure du profil vertical de vitesse :
A l'ordre suivant (ordre
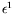 ) et en utilisant les résultats
ci-dessus, il vient par la même démarche :
où
) et en utilisant les résultats
ci-dessus, il vient par la même démarche :
où 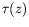 est un polynôme en
est un polynôme en 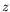 qui traduit la structure du
profil vertical de température ; son expression dépend du type de
conditions aux limites thermiques en
qui traduit la structure du
profil vertical de température ; son expression dépend du type de
conditions aux limites thermiques en 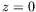 et
et 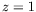 . Suivant le choix
d'un fond conducteur ou isolant, nous obtenons :
Aux ordres suivants, il ne reste que des systèmes d'équations
dont les solutions sont triviales :
La méthode perturbative en
. Suivant le choix
d'un fond conducteur ou isolant, nous obtenons :
Aux ordres suivants, il ne reste que des systèmes d'équations
dont les solutions sont triviales :
La méthode perturbative en
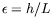 donne donc un résultat
exact dans le cas rectangulaire, et fournit un moyen simple d'obtenir
l'écoulement de base :
donne donc un résultat
exact dans le cas rectangulaire, et fournit un moyen simple d'obtenir
l'écoulement de base :
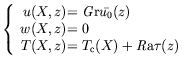 |
(1.7) |
Figure:
Profils verticaux
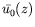 (à gauche) et
(à gauche) et 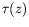 (à droite, pour
(à droite, pour
 =0) décrivant complètement
l'écoulement de base en géométrie cartésienne.
=0) décrivant complètement
l'écoulement de base en géométrie cartésienne.
|
|
Les profils verticaux correspondants sont reproduits sur la
figure ![[*]](crossref.png) . L'absence de vitesse verticale
. L'absence de vitesse verticale  est la
traduction du rejet des parois à l'infini : l'écoulement de base a
ainsi été déterminé dans le cas d'une couche de fluide de
longueur infinie ; la prise en compte des conditions aux limites sur les
parois latérales introduirait l'existence d'une vitesse verticale
près des bords, et un raccordement des solutions comme effectué par
Sen et Davis (1982) devrait alors être envisagé.
est la
traduction du rejet des parois à l'infini : l'écoulement de base a
ainsi été déterminé dans le cas d'une couche de fluide de
longueur infinie ; la prise en compte des conditions aux limites sur les
parois latérales introduirait l'existence d'une vitesse verticale
près des bords, et un raccordement des solutions comme effectué par
Sen et Davis (1982) devrait alors être envisagé.
Remarque : A partir de l'expression de la vitesse ainsi obtenue,
il est possible d'avoir accès à la vitesse en surface dans le cas
purement thermocapillaire (
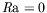 ). Nous trouvons alors :
). Nous trouvons alors :
Ce qui est à rapprocher de l'expression (![[*]](crossref.png) ),
trouvée « à la main » ; l'ordre de grandeur alors trouvé est
très correct.
),
trouvée « à la main » ; l'ordre de grandeur alors trouvé est
très correct.




suivant: 1.2.3 Géométrie cylindrique
monter: 1.2 Calcul de l'écoulement
précédent: 1.2.1.3 Adimensionalisation et petit
Table des matières
Nicolas Garnier - Thèse de doctorat


![]() selon la direction du gradient
(figure
selon la direction du gradient
(figure ![[*]](crossref.png) ) et nous notons l'abscisse
adimensionnée
) et nous notons l'abscisse
adimensionnée
![]() . Ainsi, la variable
. Ainsi, la variable ![]() sera
une variable « lente » par rapport à la variable
sera
une variable « lente » par rapport à la variable ![]() .
.
![]() ; la résolution aux ordres suivants
s'effectue de la même façon. A l'ordre 0 en
; la résolution aux ordres suivants
s'effectue de la même façon. A l'ordre 0 en ![]() , le
système d'équations s'écrit :
, le
système d'équations s'écrit :
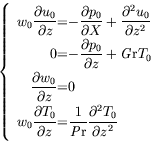
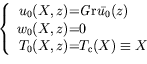
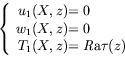
![\begin{displaymath}\left\vert
\begin{array}{ll}
\tau(z) = \displaystyle \frac{...
...ght] & \quad \text{si fond isolant} \\
\end{array} \right.
\end{displaymath}](img199.png)
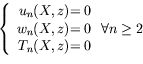
![\includegraphics[width=7cm]{U}](img203.png)
![\includegraphics[width=7cm]{T}](img204.png)
![[*]](crossref.png) . L'absence de vitesse verticale
. L'absence de vitesse verticale ![]() ). Nous trouvons alors :
). Nous trouvons alors :
![[*]](crossref.png) ),
trouvée « à la main » ; l'ordre de grandeur alors trouvé est
très correct.
),
trouvée « à la main » ; l'ordre de grandeur alors trouvé est
très correct.