



suivant: 1.2.2 Géométrie rectangulaire
monter: 1.2.1 Equations de Boussinesq
précédent: 1.2.1.2 Conditions aux limites
Table des matières
1.2.1.3 Adimensionalisation et petit paramètre géométrique
Comme nous l'avons déjà évoqué, les symétries imposent que
l'écoulement de base soit indépendant de la direction horizontale
transverse au gradient de température, et que la vitesse selon cette
direction soit nulle :
Pour calculer l'écoulement de base, nous employons une méthode
perturbative utilisant le petit paramètre
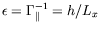 . Les expressions de l'écoulement de
base que nous obtenons sont alors celles d'une géométrie infinie
selon la direction du gradient. Ce développement suivant le rapport
d'aspect n'est pas nécessaire dans le cas rectangulaire où une
solution exacte peut être trouvée directement, mais très pratique
pour aborder le cas cylindrique. Nous choisissons alors les échelles
suivantes :
. Les expressions de l'écoulement de
base que nous obtenons sont alors celles d'une géométrie infinie
selon la direction du gradient. Ce développement suivant le rapport
d'aspect n'est pas nécessaire dans le cas rectangulaire où une
solution exacte peut être trouvée directement, mais très pratique
pour aborder le cas cylindrique. Nous choisissons alors les échelles
suivantes :
| température |
 |
| longueur dans la direction du gradient |
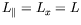 |
| longueur dans la direction verticale |
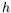 |
vitesse (pour 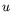 et et 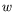 ) ) |
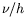 |
| pression |
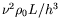 |
| masse volumique |
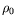 |
La partie hydrostatique de la pression correspondant à la masse
volumique 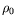 est de plus soustraite de la nouvelle expression de
la pression.
est de plus soustraite de la nouvelle expression de
la pression.




suivant: 1.2.2 Géométrie rectangulaire
monter: 1.2.1 Equations de Boussinesq
précédent: 1.2.1.2 Conditions aux limites
Table des matières
Nicolas Garnier - Thèse de doctorat
![]() est de plus soustraite de la nouvelle expression de
la pression.
est de plus soustraite de la nouvelle expression de
la pression.