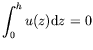1.2.1.2 Conditions aux limites

Nous devons écrire les conditions aux limites pour la vitesse et la température dans la direction verticale $z$. Les conditions limites sur les bords latéraux (direction $\vec{e}_\parallel=\vec{e}_x$ et $\vec{e}_\perp=\vec{e}_y$) sont rejetées à l'infini et n'interviennent donc pas : nous étudions un système d'extension horizontale infinie.

Nous supposons de plus que la surface libre est indéformable : $\mathit S\xspace \rightarrow \infty$.

Les deux directions horizontales sont ici formellement équivalentes ; nous avons :

en $z=0$ :	condition cinématique : $\vec{v}\vert _{z=0}=\vec{0}$
	condition thermique : $\left\vert { \begin{tabular}{rll} \medskip $T\vert _{z=0}$\ & $= T_c $ &... ...t _{z=0}$\ & = 0 & $\text{si paroi isolante}$\ \\ \end{tabular} } \right.$
en $z=h$ :	condition cinématique normale : $\vec{n}.\vec{v} = 0$   i.e.$\quad w\vert _{z=h}=0$
	condition cinématique tangentielle selon $\vec{e}_x$ : $$\frac{\partial \sigma}{\partial x} = \eta \left( \displaystyle \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}\right)$$
	condition thermique : $$\left. \frac{\partial T}{\partial z}\right\vert _{z=h} + \mathit B{\mathrm i}\xspace (T-T_{\text a})= -Q$$

où l'on a noté $Q$ le flux de chaleur à la surface -- que nous supposerons nul -- et $T_{\text a}$ la température de l'air loin au dessus de la surface. Nous supposons que $T_{\text a} = T_{\text c}(x)$ = le profil conducteur de température. $\mathit B{\mathrm i}\xspace$ est alors le nombre de Biot^1.2 et nous posons dans la suite $\mu=\mathit B{\mathrm i}\xspace /(1+\mathit B{\mathrm i}\xspace )$.

Remarque : Ecrire et résoudre l'équation de conservation de la matière est équivalent dans notre système à écrire :

$$\int_0^h u(z) \mathrm dz = 0$$