- ...
Curie1.1
- Une forme de ce principe s'exprime ainsi : « Les effets
sont au moins aussi symétriques que les causes qui leur ont donné
naissance ».
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Biot1.2
- En notant
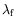 et
et
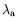 les
conductivités thermiques du fluide (huile) et de l'air, et
les
conductivités thermiques du fluide (huile) et de l'air, et
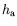 la hauteur d'air considéré entre la surface libre et l'altitude
dont on connaît le profil
la hauteur d'air considéré entre la surface libre et l'altitude
dont on connaît le profil
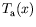 , le nombre de Biot peut
être écrit :
où
, le nombre de Biot peut
être écrit :
où 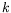 est le nombre d'onde de la structure convective.
est le nombre d'onde de la structure convective.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... base1.3
- L'écoulement de base
en géométrie rectangulaire (
![[*]](crossref.png) ) n'est qu'un cas limite
de (
) n'est qu'un cas limite
de (![[*]](crossref.png) ) lorsque la courbure devient négligeable :
) lorsque la courbure devient négligeable :
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... m\'ecanique1.4
- Cette contrainte
a par exemple pour origine un vent de vitesse uniforme ; il est
remarquable que les équations en volume soient les mêmes que dans
notre problème thermocapillaire, ainsi que les conditions aux limites
mécaniques. Notre système diffère « juste » par l'adjonction de
la variable
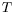 et les conditions aux limites thermiques enrichissent le
problème jusqu'à le rendre très différent de celui du vent en
surface.
et les conditions aux limites thermiques enrichissent le
problème jusqu'à le rendre très différent de celui du vent en
surface.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
obtient1.5
- Cette écriture est correcte si
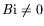 . Dans le
cas d'un nombre de Biot nul, des termes supplémentaires de même
structure que les termes de pression doivent être pris en compte. Ils
traduisent l'existence d'un champ de température à grande échelle.
En effet,
. Dans le
cas d'un nombre de Biot nul, des termes supplémentaires de même
structure que les termes de pression doivent être pris en compte. Ils
traduisent l'existence d'un champ de température à grande échelle.
En effet,
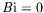 simplifie l'expression des conditions aux limites
thermiques à la surface et entraîne donc l'existence d'une
constante d'intégration non fixée. Nous avons réservé aux termes
de température correspondants le même sort que pour les termes de
pression... nous les négligeons.
simplifie l'expression des conditions aux limites
thermiques à la surface et entraîne donc l'existence d'une
constante d'intégration non fixée. Nous avons réservé aux termes
de température correspondants le même sort que pour les termes de
pression... nous les négligeons.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... propri\'et\'es2.1
- Pour la tension de surface : 1
dyne/cm =
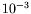 N/m.
N/m.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2.12.2
- Pour la viscosité : 1 cSt =
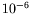 m
m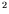 /s.
/s.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Alumel/Chromel2.3
- L'Alumel (Ni-Al,
magnétique) constitue le conducteur de la borne (-) alors que le
conducteur à la borne (+) est en Chromel (Ni-Cr). La sensibilité
d'une jonction est de 41.3
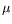 V/K à 20
V/K à 20 C (données
constructeur).
C (données
constructeur).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
\'etudie2.4
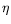 est relié au paramètre d'ordre de
l'instabilité en ondes hydrothermales :
est relié au paramètre d'ordre de
l'instabilité en ondes hydrothermales :
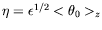 , où
, où  est la distance adimensionnée au seuil
et
est la distance adimensionnée au seuil
et
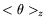 représente l'information donnée par le profil
vertical intégré dans la direction
représente l'information donnée par le profil
vertical intégré dans la direction 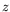 . Pour les ondes
hydrothermales,
. Pour les ondes
hydrothermales,
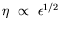 car l'instabilité est
supercritique ; on peut donc travailler avec
car l'instabilité est
supercritique ; on peut donc travailler avec 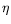 aussi petit que l'on
veut, et donc
aussi petit que l'on
veut, et donc 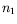 petit.
petit.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... silicones2.5
- A comparer à
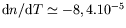 K
K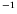 pour l'eau, d'après Merzkirch (1987).
pour l'eau, d'après Merzkirch (1987).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... hauteur2.6
- la
taille caractéristique d'un ménisque est donnée par la longueur
capillaire
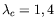 mm pour l'huile utilisée
(formule (
mm pour l'huile utilisée
(formule (![[*]](crossref.png) ))
))
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Fourier2.7
- Nos définitions sont les
suivantes :
où les intégrales sont prises sur tout l'espace accessible à la
variable d'intégration.
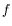 est la fréquence,
est la fréquence,
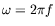 la
pulsation et
la
pulsation et 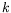 le nombre d'onde dans la direction
le nombre d'onde dans la direction  . Comme nos
signaux sont discrets en espace et en temps, les intégrales sont
remplacées par des sommes finies.
. Comme nos
signaux sont discrets en espace et en temps, les intégrales sont
remplacées par des sommes finies.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cas2.8
- Cette valeur moyenne correspond en fait
à l'éclairage moyen du pixel
 au cours du temps. La distribution
spatiale de cette valeur reflète l'inhomogénéité spatiale de
l'éclairage incident, la présence de poussière sur les lentilles
et miroirs, les déviations du faisceau par l'écoulement de base
-- avec où sans rouleaux stationnaires corotatifs --, et
éventuellement la présence d'autres structures stationnaires.
au cours du temps. La distribution
spatiale de cette valeur reflète l'inhomogénéité spatiale de
l'éclairage incident, la présence de poussière sur les lentilles
et miroirs, les déviations du faisceau par l'écoulement de base
-- avec où sans rouleaux stationnaires corotatifs --, et
éventuellement la présence d'autres structures stationnaires.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Dirichlet3.1
- Le
cas de conditions de Neumann est aussi possible :
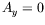 en
en 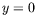 et
et
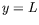 . Cela modifie peu la structure des résultats.
. Cela modifie peu la structure des résultats.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... grande3.2
- Rappelons :
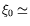 5.1
mm.
5.1
mm.  =502 mm (resp. 180 mm) pour l'anneau (resp. le rectangle). Donc
=502 mm (resp. 180 mm) pour l'anneau (resp. le rectangle). Donc
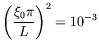
(resp.
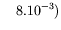
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Tobias-D:983.3
- L'article de Tobias et al. (1998) contient une
petite erreur dans l'expression du coefficient de proportionalité de
l'amplitude, mais cela ne change pas du tout la conclusion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
directes3.4
- Nous employons une méthode de type Runge-Kutta
d'ordre 4 avec 256 points en espace.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bords3.5
- Le cas de conditions aux
limites différentes peut d'ailleurs permettre une non-annulation de
l'amplitude au profil de ses dérivées spatiales ; nous n'avons pas
exploré analytiquement ce cas car il nous semblait plus éloigné
des observations expérimentales.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... \'ecrire3.6
- Nous pouvons
aussi prendre en compte la saturation non-linéaire en supposant que
l'amplitude répond à une équation de Landau dans le cas
stationnaire :
Nous trouvons alors :
ce qui est semblable au résultat exposé.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... source3.7
- Dans le
cas de l'instabilité primaire, nous n'avions pas observé des
structures analoques car les sources n'étaient pas assez bruyantes
et/ou la cellule pas assez longue.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 3.8
3.8
- Cette dépendance a été
mise en évidence dans l'anneau et l'ajout de termes supplémentaires
à l'équation de
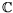 GL permet de la décrire (cf
annexe
GL permet de la décrire (cf
annexe ![[*]](crossref.png) ). Nous la retrouvons dans le rectangle comme
le montre la figure
). Nous la retrouvons dans le rectangle comme
le montre la figure ![[*]](crossref.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Hann4.1
- La fenêtre de
Hann est une fenêtre de Hamming qui s'annule exactement aux bords
contrairement à cette dernière qui prend aux bords une valeur finie,
très faible.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
horizontal5.1
- Nous pouvons remarquer que la reconnexion des ondes
cylindriques et des ondes planes s'effectue avec un pincement et/ou une
dilatation localisée de la structure ; cette modification locale du
nombre d'onde conduit parfois à l'existence d'une dislocation spatiale
dont le comportement spatio-temporel peut être périodique. C'est
l'étude d'un tel objet qui a été effectuée par
Burguete et al. (1999) dans des conditions expérimentales proches. Le trou
d'amplitude étudié dans cet article provient ainsi de la
déformation spatiale d'une onde de type OH2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... spatiaux5.2
- Dans le
cas d'une onde, ces harmoniques spatiaux se traduisent aussi par des
harmoniques temporels : le signal ombroscopique qui défile en un point
de l'écran n'est plus monochromatique.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
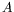 B.1
B.1
- Dans le cas d'un système de deux équations couplées,
la solution
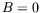 entraine l'annulation du terme de couplage et seule
subsiste une équation pour
entraine l'annulation du terme de couplage et seule
subsiste une équation pour 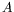 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[*]](crossref.png) ) n'est qu'un cas limite
de (
) n'est qu'un cas limite
de (![[*]](crossref.png) ) lorsque la courbure devient négligeable :
) lorsque la courbure devient négligeable :
![[*]](crossref.png) ))
))
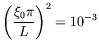 (resp.
(resp.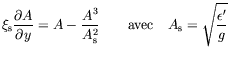
![[*]](crossref.png) ). Nous la retrouvons dans le rectangle comme
le montre la figure
). Nous la retrouvons dans le rectangle comme
le montre la figure ![[*]](crossref.png) .
.