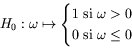suivant: 2.4.3 Choix des filtres
monter: 2.4 Analyse des signaux
précédent: 2.4.1 Recherche de la
Table des matières
Une fois la fréquence 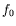 de la porteuse des ondes déterminée,
une transformée de Hilbert associée à un filtrage est appliquée
dans cette même direction à l'ensemble du diagramme. Le signal
«brut» réel, qui peut être écrit pour le mode principal :
est ainsi transformé en signal complexe équivalent :
de la porteuse des ondes déterminée,
une transformée de Hilbert associée à un filtrage est appliquée
dans cette même direction à l'ensemble du diagramme. Le signal
«brut» réel, qui peut être écrit pour le mode principal :
est ainsi transformé en signal complexe équivalent :
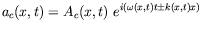
avec
![$\displaystyle ~~
A_r = \Re[A_c(x,t)]
$](img623.png)
La transformée de Hilbert correspond à un effacement des
fréquences négatives. Il s'agit donc d'un filtre linéaire
particulier appliqué au signal brut 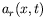 . En tant que filtrage
linéaire, il peut être interprété comme une convolution du
signal de départ avec une fonction de transfert, i.e., une
multiplication dans l'espace de Fourier :
où
. En tant que filtrage
linéaire, il peut être interprété comme une convolution du
signal de départ avec une fonction de transfert, i.e., une
multiplication dans l'espace de Fourier :
où
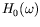 est une version particulière de la fonction d'Heavyside
qui s'annule à l'origine :
La fréquence nulle est effacée car elle correspond à la valeur
moyenne du signal le long de la colonne
est une version particulière de la fonction d'Heavyside
qui s'annule à l'origine :
La fréquence nulle est effacée car elle correspond à la valeur
moyenne du signal le long de la colonne  , ce qui n'a pas de sens
physique dans notre cas2.8.
Nous profitons de la transformée de Hilbert pour appliquer un second
filtre au signal (deux filtres linéaires commutent) afin d'éliminer
la partie du signal hors de notre propos : les harmoniques du signal de
l'onde, les signaux parasites non stationnaires (éventuelles ondes de
gravité...) et le plus de bruit possible :
Le choix du filtre
, ce qui n'a pas de sens
physique dans notre cas2.8.
Nous profitons de la transformée de Hilbert pour appliquer un second
filtre au signal (deux filtres linéaires commutent) afin d'éliminer
la partie du signal hors de notre propos : les harmoniques du signal de
l'onde, les signaux parasites non stationnaires (éventuelles ondes de
gravité...) et le plus de bruit possible :
Le choix du filtre
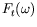 et sa construction sont détaillés
dans le paragraphe suivant.
et sa construction sont détaillés
dans le paragraphe suivant.




suivant: 2.4.3 Choix des filtres
monter: 2.4 Analyse des signaux
précédent: 2.4.1 Recherche de la
Table des matières
Nicolas Garnier - Thèse de doctorat