



suivant: 2.4.4 Second filtrage
monter: 2.4 Analyse des signaux
précédent: 2.4.2 Transformée de Hilbert
Table des matières
A distance finie du seuil d'apparition des ondes, la fréquence
est distribuée autour de la valeur 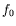 , ce qui correspond à
un paquet d'onde dans l'espace de Fourier :
, ce qui correspond à
un paquet d'onde dans l'espace de Fourier :
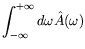
e
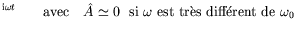
La largeur du paquet d'onde traduit la richesse du signal et doit être
conservée dans nos études. Ainsi, le filtrage doit laisser passer un
certain nombre de modes : le filtre passe-bande choisi a une largeur
adaptée à celle du pic visible sur le spectre. A cette fin, nous
utilisons un filtre linéaire réel ; nous avons rédigé une
routine permettant de construire des filtres laissant entièrement
passer une bande de modes tout en ayant des bords « doux » -- le
filtre est dérivable -- afin de minimiser la pollution du signal
filtré par des résidus de convolution. De tels filtres sont
illustrés sur la figure ![[*]](crossref.png) .
.
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) .
.