



suivant: 2.4.2 Transformée de Hilbert
monter: 2.4 Analyse des signaux
précédent: 2.4 Analyse des signaux
Table des matières
Après transformation de Fourier2.7
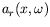 d'une colonne
d'une colonne  ,
nous avons accès à la densité spectrale de puissance
,
nous avons accès à la densité spectrale de puissance
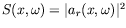 . Les fonctions
. Les fonctions
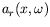 et
et
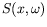 sont paires en
sont paires en 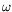 car le signal de départ est
réel. Le pic principal du spectre nous donne la fréquence
car le signal de départ est
réel. Le pic principal du spectre nous donne la fréquence 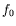 et
nous pouvons repérer les éventuelles harmoniques du signal et ses
modulations. Afin d'augmenter le rapport signal sur bruit des spectres,
nous moyennons un grand nombre d'entre eux réalisés sur
différentes colonnes du diagramme, comme expliqué sur la figure
et
nous pouvons repérer les éventuelles harmoniques du signal et ses
modulations. Afin d'augmenter le rapport signal sur bruit des spectres,
nous moyennons un grand nombre d'entre eux réalisés sur
différentes colonnes du diagramme, comme expliqué sur la figure
![[*]](crossref.png) :
Notons que cette opération est différente de celle visant à
moyenner d'abord les transformées de Fourier, puis prendre le module
du résultat.
:
Notons que cette opération est différente de celle visant à
moyenner d'abord les transformées de Fourier, puis prendre le module
du résultat.
Figure:
Exemple de diagramme spatio-temporel. En haut : cliché ombroscopique représentant
l'état étudié (ici, deux spirales en contrarotation pour  mm et
mm et
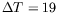 K dans la cellule LOTUS) ; la ligne blanche symbolise la ligne
d'acquisition (un cercle).
En bas : diagrammes spatio-temporels représentant le signal ombroscopique en fonction
de la position sur la ligne d'acquisition (angle
K dans la cellule LOTUS) ; la ligne blanche symbolise la ligne
d'acquisition (un cercle).
En bas : diagrammes spatio-temporels représentant le signal ombroscopique en fonction
de la position sur la ligne d'acquisition (angle 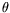 ) et du temps (seules les lignes
entre
) et du temps (seules les lignes
entre 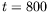 s et
s et 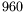 s sont représentées pour des raisons de clarté) ;
la fréquence d'acquisition est de
s sont représentées pour des raisons de clarté) ;
la fréquence d'acquisition est de 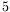 Hz.
A gauche : diagramme brut, juste après son acquisition.
A droite : diagramme filtré en temps, puis en espace de sorte à isoler
l'onde gauche, majoritaire (cf figure
Hz.
A gauche : diagramme brut, juste après son acquisition.
A droite : diagramme filtré en temps, puis en espace de sorte à isoler
l'onde gauche, majoritaire (cf figure ![[*]](crossref.png) ).
).
|
|
Figure:
Spectres issus du diagramme de la figure ![[*]](crossref.png) .
Première ligne : spectre temporel brut sur la colonne
.
Première ligne : spectre temporel brut sur la colonne 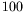 (
(
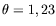 ) et spectre spatial brut sur la ligne
) et spectre spatial brut sur la ligne 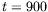 s.
Deuxième ligne : spectres moyennés avant et après le premier
filtrage en temps.
Troisième ligne : spectres moyennés après le second filtrage
en espace séparant les ondes majoritaire (gauche) et minoritaire (droite).
Dernière ligne : filtre utilisé en temps et en espace.
Noter par exemple que l'onde minoritaire n'a pas exactement la
même fréquence que l'onde majoritaire, et que cela conduit
à un pic plus large dans le spectre brut.
s.
Deuxième ligne : spectres moyennés avant et après le premier
filtrage en temps.
Troisième ligne : spectres moyennés après le second filtrage
en espace séparant les ondes majoritaire (gauche) et minoritaire (droite).
Dernière ligne : filtre utilisé en temps et en espace.
Noter par exemple que l'onde minoritaire n'a pas exactement la
même fréquence que l'onde majoritaire, et que cela conduit
à un pic plus large dans le spectre brut.
|
|
La recherche du nombre d'onde 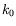 s'effectue de manière analogue en
permutant lignes et colonnes. Dans la suite, nous continuons les
descriptions à l'aide de la fréquence.
s'effectue de manière analogue en
permutant lignes et colonnes. Dans la suite, nous continuons les
descriptions à l'aide de la fréquence.
Nous verrons plus loin que des valeurs plus précises de 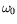 et
et
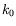 sont obtenues après transformée de Hilbert.
sont obtenues après transformée de Hilbert.




suivant: 2.4.2 Transformée de Hilbert
monter: 2.4 Analyse des signaux
précédent: 2.4 Analyse des signaux
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) :
:
![]() et
et
![]() sont obtenues après transformée de Hilbert.
sont obtenues après transformée de Hilbert.