



suivant: 3.1.1.1.6 Conditions limites finies
monter: 3.1.1.1 Forme des solutions
précédent: 3.1.1.1.4 Conditions limites périodiques
Table des matières
Dans le cas
d'un domaine de longueur  sans périodicité, nous devons
spécifier des conditions aux limites
sans périodicité, nous devons
spécifier des conditions aux limites 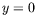 et
et 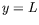 . Nous pouvons par
exemple prendre des conditions aux limites de type Dirichlet3.1 (proches des
faits expérimentaux) :
Nous résolvons le problème en recherchant une solution du type onde
plane, mais avec un nombre d'onde complexe. Nous autorisons ainsi
l'existence d'un taux de croissance spatial, inutile et inconvenant dans
les cas infinis et périodiques ; nous reprenons ainsi les calculs de
Tobias et al. (1998) mais avec une équation dimensionnée. Nous
trouvons que les solutions n'existent que pour certaines valeurs
discrètes
. Nous pouvons par
exemple prendre des conditions aux limites de type Dirichlet3.1 (proches des
faits expérimentaux) :
Nous résolvons le problème en recherchant une solution du type onde
plane, mais avec un nombre d'onde complexe. Nous autorisons ainsi
l'existence d'un taux de croissance spatial, inutile et inconvenant dans
les cas infinis et périodiques ; nous reprenons ainsi les calculs de
Tobias et al. (1998) mais avec une équation dimensionnée. Nous
trouvons que les solutions n'existent que pour certaines valeurs
discrètes
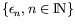 de
de  . La solution non
nulle qui apparaît pour la plus faible valeur
. La solution non
nulle qui apparaît pour la plus faible valeur
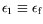 du paramètre de contrôle s'écrit :
du paramètre de contrôle s'écrit :
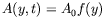 e e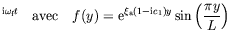 |
(3.4) |
où :
Le terme
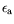 est d'ordre 1 car la vitesse de groupe est
d'ordre 1. Il traduit le décalage du seuil dû au caractère
convectif de l'instabilité au seuil et à l'attente de la transition
convectif/absolu. Par contre, la différence
est d'ordre 1 car la vitesse de groupe est
d'ordre 1. Il traduit le décalage du seuil dû au caractère
convectif de l'instabilité au seuil et à l'attente de la transition
convectif/absolu. Par contre, la différence
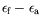 est d'ordre
est d'ordre 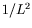 et elle ne signale que les
effets de discrétisations, très réduits dans le cas des grandes
boîtes.
et elle ne signale que les
effets de discrétisations, très réduits dans le cas des grandes
boîtes.
Dans les cas qui nous intéressent (anneau et rectangle), la taille du
système  est très grande3.2 devant
est très grande3.2 devant 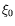 et l'on peut donc négliger les
effets de discrétisation. Nous confondons ainsi dans la suite
et l'on peut donc négliger les
effets de discrétisation. Nous confondons ainsi dans la suite
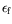 avec
avec
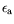 ainsi que
ainsi que
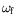 avec
avec
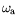 .
.
Aucune solution non nulle, i.e. aucune onde, n'existe tant que
 n'a pas atteint la valeur
n'a pas atteint la valeur
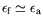 , finie, indépendante de
, finie, indépendante de  . En ce sens, la
solution trouvée pour cette valeur de
. En ce sens, la
solution trouvée pour cette valeur de  constitue un
mode global, comme défini par Huerre et Monkewitz (1990). Il est remarquable
que nous trouvions le seuil d'existence des ondes à la valeur
constitue un
mode global, comme défini par Huerre et Monkewitz (1990). Il est remarquable
que nous trouvions le seuil d'existence des ondes à la valeur
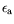 qui correspond à la transition convectif/absolu
des ondes sans invoquer l'analyse particulière (Deissler (1985) par
exemple) que requiert l'étude de cette transition.
qui correspond à la transition convectif/absolu
des ondes sans invoquer l'analyse particulière (Deissler (1985) par
exemple) que requiert l'étude de cette transition.
Ce mode global qui existe pour
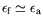 possède une enveloppe spatiale particulière,
produit d'un sinus par une exponentielle. Le sinus permet de répondre
aux conditions aux limites imposées alors que l'exponentielle traduit
l'advection par la vitesse de groupe. Lorsque
possède une enveloppe spatiale particulière,
produit d'un sinus par une exponentielle. Le sinus permet de répondre
aux conditions aux limites imposées alors que l'exponentielle traduit
l'advection par la vitesse de groupe. Lorsque
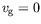 , le taux
de croissance spatial
, le taux
de croissance spatial
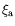 s'annule et l'exponentielle
disparaît ; la distinction convectif/absolu n'existe plus. Du coup,
le décalage de fréquence
s'annule et l'exponentielle
disparaît ; la distinction convectif/absolu n'existe plus. Du coup,
le décalage de fréquence
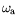 et le décalage de
nombre d'onde
et le décalage de
nombre d'onde
 i
i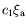 s'annulent aussi.
s'annulent aussi.




suivant: 3.1.1.1.6 Conditions limites finies
monter: 3.1.1.1 Forme des solutions
précédent: 3.1.1.1.4 Conditions limites périodiques
Table des matières
Nicolas Garnier - Thèse de doctorat
![]() est très grande3.2 devant
est très grande3.2 devant ![]() et l'on peut donc négliger les
effets de discrétisation. Nous confondons ainsi dans la suite
et l'on peut donc négliger les
effets de discrétisation. Nous confondons ainsi dans la suite
![]() avec
avec
![]() ainsi que
ainsi que
![]() avec
avec
![]() .
.
![]() n'a pas atteint la valeur
n'a pas atteint la valeur
![]() , finie, indépendante de
, finie, indépendante de ![]() . En ce sens, la
solution trouvée pour cette valeur de
. En ce sens, la
solution trouvée pour cette valeur de ![]() constitue un
mode global, comme défini par Huerre et Monkewitz (1990). Il est remarquable
que nous trouvions le seuil d'existence des ondes à la valeur
constitue un
mode global, comme défini par Huerre et Monkewitz (1990). Il est remarquable
que nous trouvions le seuil d'existence des ondes à la valeur
![]() qui correspond à la transition convectif/absolu
des ondes sans invoquer l'analyse particulière (Deissler (1985) par
exemple) que requiert l'étude de cette transition.
qui correspond à la transition convectif/absolu
des ondes sans invoquer l'analyse particulière (Deissler (1985) par
exemple) que requiert l'étude de cette transition.
![]() possède une enveloppe spatiale particulière,
produit d'un sinus par une exponentielle. Le sinus permet de répondre
aux conditions aux limites imposées alors que l'exponentielle traduit
l'advection par la vitesse de groupe. Lorsque
possède une enveloppe spatiale particulière,
produit d'un sinus par une exponentielle. Le sinus permet de répondre
aux conditions aux limites imposées alors que l'exponentielle traduit
l'advection par la vitesse de groupe. Lorsque
![]() , le taux
de croissance spatial
, le taux
de croissance spatial
![]() s'annule et l'exponentielle
disparaît ; la distinction convectif/absolu n'existe plus. Du coup,
le décalage de fréquence
s'annule et l'exponentielle
disparaît ; la distinction convectif/absolu n'existe plus. Du coup,
le décalage de fréquence
![]() et le décalage de
nombre d'onde
et le décalage de
nombre d'onde
![]() i
i![]() s'annulent aussi.
s'annulent aussi.