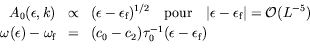3.1.1.1.6 Conditions limites finies - analyse faiblement non-linéaire

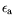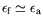Les solutions du problème non-linéaire sont plus difficiles à trouver que dans les cas précédents à cause de la translation du seuil à $\epsilon_{\text{a}}$ ; nous pouvons procéder à une analyse faiblement non-linéaire autour de la première de ces solutions, obtenue pour $\epsilon_{\text f} \simeq \epsilon_{\text a}$. Nous n'avons plus de famille continue de solutions comme dans les cas précédents.

Au voisinage de 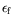$\epsilon_{\text{f}}$, nous pouvons calculer :

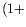
$$(1+$$i$$c_0)(\epsilon-\epsilon_{\text f}) - \text{i} \tau_0 (\omega(\epsi... ...i^4(1+c_1^2)^5 g \vert A_0\vert^2 \left(\frac{\xi_0^2}{\tau_0 v_g L}\right)^5$$

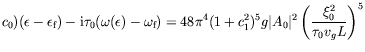
Nous trouvons donc les comportements critiques suivants, donnés par Tobias et al. (1998)^3.3, Chomaz et Couairon (1999) :

$$\begin{array}{rcl} \smallskip A_0(\epsilon,k) & \propto ... ...2) \tau_0^{-1} (\epsilon - \epsilon_{\text{f}}) \end{array}$$

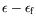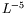L'apparition du mode global est donc supercritique et le décalage de fréquence proportionnel à $\epsilon-\epsilon_{\text f}$. Ces résultats sont accompagnés de leur zone de validité en $\epsilon$, qui est en $L^{-5}$, donc a priori très réduite, voire inobservable.