



suivant: 3.1.1.1.1 Géométrie infinie -
monter: 3.1.1 Cas de l'équation
précédent: 3.1.1 Cas de l'équation
Table des matières
Nous allons résoudre l'équation de
 GL linéarisée, puis
entière, dans chacune des trois géométries : infinie, finie
périodique, finie non périodique. Remarquons que nous ne
considérons que le problème d'une onde unique, mais cela n'est pas
limitatif dans notre cas. En effet, l'équation
GL linéarisée, puis
entière, dans chacune des trois géométries : infinie, finie
périodique, finie non périodique. Remarquons que nous ne
considérons que le problème d'une onde unique, mais cela n'est pas
limitatif dans notre cas. En effet, l'équation
 GL à l'ordre
linéaire est la même dans le cas d'une onde unique (équation
unique) ou de deux ondes (deux équations non couplées à l'ordre
linéaire). De plus, du fait du couplage non-linéaire destructif
observé au seuil des ondes hydrothermales (cf
§
GL à l'ordre
linéaire est la même dans le cas d'une onde unique (équation
unique) ou de deux ondes (deux équations non couplées à l'ordre
linéaire). De plus, du fait du couplage non-linéaire destructif
observé au seuil des ondes hydrothermales (cf
§ ![[*]](crossref.png) ), le problème non-linéaire est lui aussi
limité à l'étude d'une seule équation pour
), le problème non-linéaire est lui aussi
limité à l'étude d'une seule équation pour 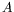 si l'on ne
regarde que l'onde dominante
si l'on ne
regarde que l'onde dominante 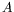 et si l'on suppose
et si l'on suppose 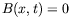 . Le cas
d'une instabilité en ondes stationnaires requiert quant à lui
l'analyse simultanée de deux équations
. Le cas
d'une instabilité en ondes stationnaires requiert quant à lui
l'analyse simultanée de deux équations
 GL couplées ; c'est le
cas notamment des travaux de Neufeld et al. (1996) qui ont montré que la
transition ondes stationnaires/onde unique était reliée à la
transition convectif/absolu.
GL couplées ; c'est le
cas notamment des travaux de Neufeld et al. (1996) qui ont montré que la
transition ondes stationnaires/onde unique était reliée à la
transition convectif/absolu.
Notons qu'en toute rigueur, le cas de la géométrie finie requiert
dès l'ordre linéaire la prise en compte de deux équations car de
deux ondes. Cela est dû aux conditions aux limites utilisées qui
peuvent coupler 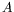 et
et 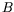 , notamment grâce à un coefficient de
réflexion (cf §
, notamment grâce à un coefficient de
réflexion (cf § ![[*]](crossref.png) ).
).
Sous-sections




suivant: 3.1.1.1.1 Géométrie infinie -
monter: 3.1.1 Cas de l'équation
précédent: 3.1.1 Cas de l'équation
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ).
).
![[*]](crossref.png) ), le problème non-linéaire est lui aussi
limité à l'étude d'une seule équation pour
), le problème non-linéaire est lui aussi
limité à l'étude d'une seule équation pour ![]() et
et ![]() , notamment grâce à un coefficient de
réflexion (cf §
, notamment grâce à un coefficient de
réflexion (cf § ![[*]](crossref.png) ).
).