next up previous contents
suivant: 3.1.1.1.3 Conditions limites périodiques monter: 3.1.1.1 Forme des solutions précédent: 3.1.1.1.1 Géométrie infinie -   Table des matières

3.1.1.1.2 Géométrie infinie - solutions non-linéaires

L'équation $ {\mathbb{C}}$GL admet un ensemble de solutions de Stokes qui s'expriment ainsi (voir par exemple Cross et Hohenberg (1993)) :

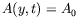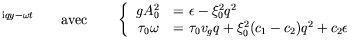$\displaystyle A(y,t) = A_0$   e$\displaystyle ^{\text{i} q y - \omega t} \qquad \text{avec} \qquad \left\{ \... ...u_0 v_g q + \xi_0^2 (c_1-c_2) q^2 + c_2 \epsilon$\ \\ \end{tabular} \right.$ (3.3)

et toujours

$\displaystyle q \in \hbox{I\hskip -2pt R}$$\displaystyle \quad \text {t.q.} \quad q^2 <\epsilon $

Ce sont tout simplement des ondes planes ([*]) dont l'amplitude et la fréquence dépendent de $ \epsilon$ et $ q$.
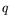Nicolas Garnier - Thèse de doctorat