suivant: 3.1.1.1.4 Conditions limites périodiques
monter: 3.1.1.1 Forme des solutions
précédent: 3.1.1.1.2 Géométrie infinie -
Table des matières
Il est
alors naturel de chercher une solution sous la forme d'une série de
Fourier (en nombres d'ondes), ce qui non seulement tient bien compte de
la périodicité spatiale mais aussi rapproche le problème du cas de
la géométrie infinie. Nous pouvons donc nous attendre à trouver un
ensemble de solutions compris dans l'ensemble des solutions ondes
planes (![[*]](crossref.png)
), mais plus réduit, de sorte à tenir
compte de l'aspect discret et non plus continu des nombres d'ondes
permis. La différence par rapport au cas de la géométrie infinie
se résume ainsi :
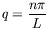
avec
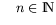
Les nombres d'ondes permis sont maintenant quantifiés.
Nicolas Garnier - Thèse de doctorat