



suivant: 3.1.1.1.2 Géométrie infinie -
monter: 3.1.1.1 Forme des solutions
précédent: 3.1.1.1 Forme des solutions
Table des matières
Il est naturel de
chercher une solution sous la forme d'une onde plane. Nous obtenons
ainsi une relation de dispersion :
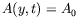 e e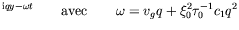 |
(3.2) |
avec
ce qui traduit l'existence d'un continuum de solutions possibles dès
que
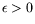 .
.
Nicolas Garnier - Thèse de doctorat