



suivant: 3.1.3 Cas de l'expérience
monter: 3.1 Instabilité primaire en
précédent: 3.1.1.2.4 - Conditions limites
Table des matières
3.1.2 Cas de l'expérience anneau
La hauteur de fluide est dans toute cette section égale à
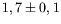 mm. La bifurcation vers le régime d'ondes est supercritique,
comme on peut le voir sur la figure
mm. La bifurcation vers le régime d'ondes est supercritique,
comme on peut le voir sur la figure ![[*]](crossref.png) , et la
structure qui apparaît possède au seuil 54 ou 55 longueurs
d'ondes. Nous en déduisons que le nombre d'onde critique
, et la
structure qui apparaît possède au seuil 54 ou 55 longueurs
d'ondes. Nous en déduisons que le nombre d'onde critique 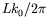 est compris entre ces deux entiers ; sa valeur en unités usuelles est
de 0,68 mm
est compris entre ces deux entiers ; sa valeur en unités usuelles est
de 0,68 mm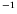 Le seuil des ondes hydrothermales est alors mesuré
avec une bonne précision grâce aux mesures de l'amplitude des modes
54 et 55 :
Le seuil des ondes hydrothermales est alors mesuré
avec une bonne précision grâce aux mesures de l'amplitude des modes
54 et 55 :
Figure:
Evolution de l'amplitude 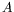 (en bas, au carré) et de la fréquence
(en bas, au carré) et de la fréquence 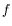 (en haut)
au voisinage du seuil dans l'anneau pour
(en haut)
au voisinage du seuil dans l'anneau pour 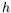 =1,7 mm.
Ces mesures correspondent à une amplitude strictement homogène dans
toute la cellule.
Les symboles
=1,7 mm.
Ces mesures correspondent à une amplitude strictement homogène dans
toute la cellule.
Les symboles 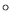 et
et  représentent respectivement les
modes 54 et 55 car
représentent respectivement les
modes 54 et 55 car
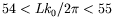 .
L'ajustement linéaire de
.
L'ajustement linéaire de 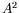 est effectué sur l'ensemble des
deux jeux de valeurs.
est effectué sur l'ensemble des
deux jeux de valeurs.
|
|
Cela correspond à un nombre de Marangoni de l'ordre de
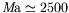 . Cette valeur du seuil nous permet de définir
. Cette valeur du seuil nous permet de définir
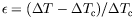 pour la cellule
annulaire, mais aussi pour la cellule rectangulaire lorsque celle-ci
contient une couche de fluide de même rapport d'aspect
pour la cellule
annulaire, mais aussi pour la cellule rectangulaire lorsque celle-ci
contient une couche de fluide de même rapport d'aspect
 selon
selon 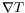 , et de même hauteur
, et de même hauteur 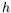 . Ce point
est discuté plus loin (§
. Ce point
est discuté plus loin (§ ![[*]](crossref.png) ).
).
Pour
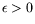 , i.e.,
, i.e.,
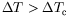 , et à
proximité du seuil, une onde unique d'amplitude stationnaire et
homogène dans la cellule est présente ; la fréquence est finie au
seuil (figure
, et à
proximité du seuil, une onde unique d'amplitude stationnaire et
homogène dans la cellule est présente ; la fréquence est finie au
seuil (figure ![[*]](crossref.png) ). L'onde minoritaire n'est pas
observée. Cette configuration nécessite éventuellement un régime
transitoire -- de l'ordre de l'heure -- pour s'établir, mais
représente le seul état le plus stable du système. Bien sûr,
l'onde observée est indifféremment une onde droite ou gauche et la
symétrie brisée est restaurée en moyenne sur l'ensemble des
réalisations. Nous pouvons déduire de ce comportement que le
couplage non-linéaire entre les deux ondes contra-propagatives est
dans notre cas destructif ; en termes d'équations d'amplitude
couplées (cf. §
). L'onde minoritaire n'est pas
observée. Cette configuration nécessite éventuellement un régime
transitoire -- de l'ordre de l'heure -- pour s'établir, mais
représente le seul état le plus stable du système. Bien sûr,
l'onde observée est indifféremment une onde droite ou gauche et la
symétrie brisée est restaurée en moyenne sur l'ensemble des
réalisations. Nous pouvons déduire de ce comportement que le
couplage non-linéaire entre les deux ondes contra-propagatives est
dans notre cas destructif ; en termes d'équations d'amplitude
couplées (cf. § ![[*]](crossref.png) ), le coefficient
), le coefficient 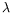 doit ainsi
être supérieur à l'unité. Des expériences appropriées (cf.
Annexe
doit ainsi
être supérieur à l'unité. Des expériences appropriées (cf.
Annexe ![[*]](crossref.png) ) nous donnent la valeur
) nous donnent la valeur
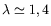 .
.
Le nombre d'onde moyen est évidemment discret, mais le nombre d'onde
local est uniforme dans la cellule (du moins tant que
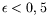 et
que les instabilités secondaires n'entrent pas en jeu). Comme nous
l'avons dit, sa valeur au seuil hésite suivant les réalisations
entre 54 et 55 ; des états homogènes avec d'autres valeurs de
et
que les instabilités secondaires n'entrent pas en jeu). Comme nous
l'avons dit, sa valeur au seuil hésite suivant les réalisations
entre 54 et 55 ; des états homogènes avec d'autres valeurs de 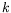 sont aussi possibles, et sont obtenus soit par perturbations, soit par
augmentation de
sont aussi possibles, et sont obtenus soit par perturbations, soit par
augmentation de  en rencontrant l'instabilité d'Eckhaus (cf.
annexe
en rencontrant l'instabilité d'Eckhaus (cf.
annexe ![[*]](crossref.png) ).
).
Figure:
Evolution de la vitesse de groupe dans l'anneau pour 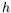 =1,7 mm.
Les symboles
=1,7 mm.
Les symboles  et
et  représentent respectivement les
modes 54 et 55.
représentent respectivement les
modes 54 et 55.
|
|
La figure ![[*]](crossref.png) illustre le comportement de la
vitesse de groupe pour les modes 54 et 55 en fonction de
illustre le comportement de la
vitesse de groupe pour les modes 54 et 55 en fonction de  ;
cette dernière est mesurée comme la vitesse des perturbations
linéaires. Nous notons ainsi que la vitesse de groupe est finie au
seuil et augmente légèrement lorsque l'on s'en éloigne. C'est la
valeur au seuil qui apparaît dans l'équation d'amplitude ; nous
avons ainsi
;
cette dernière est mesurée comme la vitesse des perturbations
linéaires. Nous notons ainsi que la vitesse de groupe est finie au
seuil et augmente légèrement lorsque l'on s'en éloigne. C'est la
valeur au seuil qui apparaît dans l'équation d'amplitude ; nous
avons ainsi
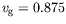 mm/s.
mm/s.




suivant: 3.1.3 Cas de l'expérience
monter: 3.1 Instabilité primaire en
précédent: 3.1.1.2.4 - Conditions limites
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) , et la
structure qui apparaît possède au seuil 54 ou 55 longueurs
d'ondes. Nous en déduisons que le nombre d'onde critique
, et la
structure qui apparaît possède au seuil 54 ou 55 longueurs
d'ondes. Nous en déduisons que le nombre d'onde critique ![\includegraphics[width=8cm]{ann-A2DT}](img710.png)
![[*]](crossref.png) ).
).
![]() , i.e.,
, i.e.,
![]() , et à
proximité du seuil, une onde unique d'amplitude stationnaire et
homogène dans la cellule est présente ; la fréquence est finie au
seuil (figure
, et à
proximité du seuil, une onde unique d'amplitude stationnaire et
homogène dans la cellule est présente ; la fréquence est finie au
seuil (figure ![[*]](crossref.png) ). L'onde minoritaire n'est pas
observée. Cette configuration nécessite éventuellement un régime
transitoire -- de l'ordre de l'heure -- pour s'établir, mais
représente le seul état le plus stable du système. Bien sûr,
l'onde observée est indifféremment une onde droite ou gauche et la
symétrie brisée est restaurée en moyenne sur l'ensemble des
réalisations. Nous pouvons déduire de ce comportement que le
couplage non-linéaire entre les deux ondes contra-propagatives est
dans notre cas destructif ; en termes d'équations d'amplitude
couplées (cf. §
). L'onde minoritaire n'est pas
observée. Cette configuration nécessite éventuellement un régime
transitoire -- de l'ordre de l'heure -- pour s'établir, mais
représente le seul état le plus stable du système. Bien sûr,
l'onde observée est indifféremment une onde droite ou gauche et la
symétrie brisée est restaurée en moyenne sur l'ensemble des
réalisations. Nous pouvons déduire de ce comportement que le
couplage non-linéaire entre les deux ondes contra-propagatives est
dans notre cas destructif ; en termes d'équations d'amplitude
couplées (cf. § ![[*]](crossref.png) ), le coefficient
), le coefficient ![]() doit ainsi
être supérieur à l'unité. Des expériences appropriées (cf.
Annexe
doit ainsi
être supérieur à l'unité. Des expériences appropriées (cf.
Annexe ![[*]](crossref.png) ) nous donnent la valeur
) nous donnent la valeur
![]() .
.
![]() et
que les instabilités secondaires n'entrent pas en jeu). Comme nous
l'avons dit, sa valeur au seuil hésite suivant les réalisations
entre 54 et 55 ; des états homogènes avec d'autres valeurs de
et
que les instabilités secondaires n'entrent pas en jeu). Comme nous
l'avons dit, sa valeur au seuil hésite suivant les réalisations
entre 54 et 55 ; des états homogènes avec d'autres valeurs de ![]() sont aussi possibles, et sont obtenus soit par perturbations, soit par
augmentation de
sont aussi possibles, et sont obtenus soit par perturbations, soit par
augmentation de ![]() en rencontrant l'instabilité d'Eckhaus (cf.
annexe
en rencontrant l'instabilité d'Eckhaus (cf.
annexe ![[*]](crossref.png) ).
).
![\includegraphics[width=8cm]{ann-vgdt}](img721.png)
![[*]](crossref.png) illustre le comportement de la
vitesse de groupe pour les modes 54 et 55 en fonction de
illustre le comportement de la
vitesse de groupe pour les modes 54 et 55 en fonction de