3.1.1.2.4  - Conditions limites finies, cas de deux ondes

Jusqu'à présent, nous n'avons considéré que le cas d'une onde unique et ainsi étudié une équation de Ginzburg-Landau pour l'amplitude 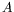$A$. Or comme nous l'avons évoqué au premier chapitre et allons le voir en §  ci-dessous, les ondes hydrothermales apparaissent par paire {onde droite, onde gauche} et il nous faut donc en toute rigueur considérer le cas de deux ondes couplées non-linéairement par deux équations d'amplitude (cf ).

Néanmoins, le couplage observé entre les deux ondes contra-propagatives est du type destructif : l'onde majoritaire se nourrit de l'onde minoritaire. De plus, l'étude que nous avons présentée ci-dessus dans le cas de la boîte finie est essentiellement linéaire : le couplage n'intervient pas dans l'équation. En fait, le seul couplage digne d'intérêt dans notre cas est celui introduit par les conditions aux limites, et il n'intervient donc que dans le cas de la boîte finie non-périodique.

Ce couplage est introduit par l'existence de coefficients de réflexion aux bords de la cellule qui permettent à l'onde incidente sur un bord d'être en partie reémise -- réfléchie -- sous forme d'onde inverse. Ce mécanisme a été introduit pour la première fois par Cross (1986) et nous discuterons son application à notre cas en § . Notons dès à présent qu'il est ici négligeable, ou du moins que le mécanisme convectif/absolu intervient « avant » et que c'est donc bien ce dernier qui pilote la dynamique au seuil d'apparition des ondes.