1.4.2 Equations d'amplitude en géométrie 1D

Plaçons-nous dans le cas d'une géométrie cartésienne 1D. Celle-ci représente pour nous la direction horizontale $\vec{e}_\perp$ orthogonale au gradient de température. Le cas limite de la géométrie 1D permet de traiter par la même équation le cas du rectangle étendu 1D et le cas de l'anneau étendu 1D.

Notre approche est différente de celle de Smith : au lieu de partir du jeu d'équations de Navier-Stokes, nous écrivons phénoménologiquement les équations d'amplitude pour $A$ et $B$ en nous servant uniquement d'arguments de symétrie. Pour une bifurcation de Hopf supercritique à 1D, si $y$ est la direction spatiale dans laquelle se déploient les ondes, nous pouvons écrire directement :

$$\left\{ \begin{array}{r@{}l} \medskip \tau_0 \left( \d... ...vert^2 + \lambda\vert A\vert^2)B \\ \end{array} \right.$$

Ces deux équations sont des équations de Ginzburg-Landau complexes d'ordre 3, présentées sous leur forme dimensionnée. Seuls les termes non-linéaires résonnants (permis par les symétries) d'ordre le plus bas sont conservés. Les coefficients de l'équation sont a priori complexes dans le cas d'une instabilité en ondes (la symétrie de translation continue dans le temps n'existe pas au contraire du cas d'une structure stationnaire). Les parties réelles des coefficients peuvent s'interpréter comme suit : $\epsilon$ est l'écart au seuil adimensionné, $\tau_0$ l'échelle de temps, $\xi_0$ la longueur de corrélation de la structure, $g$ une unité de mesure des amplitudes et $\Re(\lambda)$ un coefficient de couplage non-linéaire ; $v_g$ est la vitesse de groupe. Les parties imaginaires $c_i$ des coefficients agissent sur la fréquence et traduisent la dispersion : $c_0$ représente un éventuel décalage de fréquence avec $\epsilon$, $c_1$ la dispersion linéaire par le nombre d'onde et $c_2$ la dispersion non-linéaire par l'amplitude.

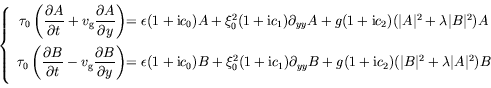
Cette approche ne donne hélas aucune information sur les coefficients. Un des fils directeurs des travaux rapportés ici est ainsi de déterminer expérimentalement les valeurs de ces coefficients. Cela a été effectué à une dimension d'espace (pour des raisons de simplicité) et nous a permis de tester la modélisation en étudiant des effets alors prédictibles et descriptibles aisément dans ce formalisme.

Notons que les équations de ${\mathbb{C}}$GL sont souvent présentées sous une forme adimensionnée. Nous avons choisi ici la forme dimensionnée afin de rester au plus près des interprétations expérimentales, par exemple en n'oubliant pas de coefficient lors des comparaisons avec les prédictions du modèle. Les adimensionalisations suivantes sont possibles :

temps	$\tau_0$	$\tau_0 \epsilon^{-1}$
espace	$\xi_0$	$\xi_0 \epsilon^{-1/2}$
vitesse	$\xi_0 \tau_0^{-1}$	$\xi_0 \tau_0^{-1} \epsilon^{1/2}$
amplitude	$g^{-1/2}$	$g^{-1/2} \epsilon^{1/2}$

Ces adimensionalisations ne conservent que les coefficients de dispersion $c_i$ et, dans le premier cas, le paramètre de contrôle $\epsilon$.

La formulation en équations d'amplitude a déjà prouvé son efficacité pour aborder les problèmes d'instabilité et formations de structures. Nous nous attacherons à éprouver ce formalisme, quitte à le pousser dans certains de ses retranchements ; ainsi nous n'hésiterons pas à transposer les résultats classiques en coordonnées cartésiennes vers les coordonnées cylindriques ; nous étudierons l'effet d'une seconde dimension d'espace et surtout nous nous autoriserons des excursions loin du seuil de l'instabilité, là où la validité des équations d'amplitude n'est pas acquise.