



suivant: 1.4.1 Développement en échelles
monter: 1. Les ondes hydrothermales
précédent: 1.3.6 Caractère absolu ou
Table des matières
1.4 Une modélisation idoine et universelle
Les informations apportées par l'analyse de stabilité linéaire ne
nous renseignent que sur quelques caractéristiques de l'instabilité
(taux de croissance linéaire, nombre de Marangoni critique,
fréquence et nombre d'onde critiques), et ce pour une valeur bien
déterminée de la différence de température. Dans de nombreux
cas, ces informations sont déjà suffisantes ou difficiles à
obtenir. Néanmoins, si l'on désire en savoir plus -- notamment sur
les dépendances vis à vis du paramètre de contrôle, ici  -- il est nécessaire d'utiliser un autre outil : l'analyse
faiblement non-linéaire. Nous allons décrire cette approche et ses
résultats, puis nous inspirer de ces derniers pour écrire une
équation modèle sous la forme d'une équation d'amplitude. Nous
discuterons alors de sa validité et de sa généricité avant
d'évoquer quelques généralisations possibles.
-- il est nécessaire d'utiliser un autre outil : l'analyse
faiblement non-linéaire. Nous allons décrire cette approche et ses
résultats, puis nous inspirer de ces derniers pour écrire une
équation modèle sous la forme d'une équation d'amplitude. Nous
discuterons alors de sa validité et de sa généricité avant
d'évoquer quelques généralisations possibles.
Il arrivera dans la suite que nous parlions d'ondes alors que seule leur
amplitude sera en fait considérée : nous écartons alors
artificiellement les dépendances « rapides » en temps et en espace
que sont les oscillations à la fréquence au seuil 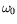 , et
avec le vecteur d'onde au seuil
, et
avec le vecteur d'onde au seuil
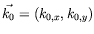 . Ainsi,
pour décrire un champ oscillant
. Ainsi,
pour décrire un champ oscillant
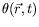 tel que la
température, nous écrivons implicitement :
tel que la
température, nous écrivons implicitement :
où
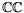 désigne le complexe conjugué du terme le
précédant. Notre propos porte alors sur les amplitudes
désigne le complexe conjugué du terme le
précédant. Notre propos porte alors sur les amplitudes 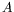 et
et 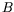 ,
lentement variables en temps et en espace via
,
lentement variables en temps et en espace via 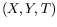 . Pour décrire
les comportements du champ oscillant, ces amplitudes sont plus
appropriées qu'une fonction particulière
. Pour décrire
les comportements du champ oscillant, ces amplitudes sont plus
appropriées qu'une fonction particulière 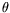 telle que la
température, les composantes de la vitesse, la pression où la
déflection de la surface si le modèle la prend en compte.
telle que la
température, les composantes de la vitesse, la pression où la
déflection de la surface si le modèle la prend en compte.
Notation : Nous écrivons 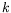 un nombre d'onde de la structure,
un nombre d'onde de la structure,
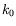 la valeur critique de ce nombre d'onde et
la valeur critique de ce nombre d'onde et 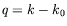 le nombre
d'onde associé aux variations de l'amplitude. De même, la
fréquence des ondes hydrothermales est notée
le nombre
d'onde associé aux variations de l'amplitude. De même, la
fréquence des ondes hydrothermales est notée
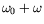 où
où
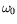 est la fréquence critique. Lorsque seul l'état de base
est présent, nous avons
est la fréquence critique. Lorsque seul l'état de base
est présent, nous avons
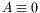 ,
,
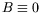 et nous l'appelons
l'état de repos.
et nous l'appelons
l'état de repos.
Sous-sections




suivant: 1.4.1 Développement en échelles
monter: 1. Les ondes hydrothermales
précédent: 1.3.6 Caractère absolu ou
Table des matières
Nicolas Garnier - Thèse de doctorat
![]() , et
avec le vecteur d'onde au seuil
, et
avec le vecteur d'onde au seuil
![]() . Ainsi,
pour décrire un champ oscillant
. Ainsi,
pour décrire un champ oscillant
![]() tel que la
température, nous écrivons implicitement :
tel que la
température, nous écrivons implicitement :
![]() un nombre d'onde de la structure,
un nombre d'onde de la structure,
![]() la valeur critique de ce nombre d'onde et
la valeur critique de ce nombre d'onde et ![]() le nombre
d'onde associé aux variations de l'amplitude. De même, la
fréquence des ondes hydrothermales est notée
le nombre
d'onde associé aux variations de l'amplitude. De même, la
fréquence des ondes hydrothermales est notée
![]() où
où
![]() est la fréquence critique. Lorsque seul l'état de base
est présent, nous avons
est la fréquence critique. Lorsque seul l'état de base
est présent, nous avons
![]() ,
,
![]() et nous l'appelons
l'état de repos.
et nous l'appelons
l'état de repos.