



suivant: 1.4 Une modélisation idoine
monter: 1.3 Analyse de stabilité
précédent: 1.3.5.4 Conclusion
Table des matières
L'instabilité qui nous intéresse est en ondes propagatives, avec une
vitesse de groupe a priori finie. Ainsi lorsque l'écart au seuil
adimensioné
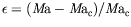 (paramètre de contrôle) est encore très faible et qu'il en est de
même du taux de croissance temporel de l'onde, l'instabilité est
convective.
(paramètre de contrôle) est encore très faible et qu'il en est de
même du taux de croissance temporel de l'onde, l'instabilité est
convective.
La notion d'instabilité convective a été introduite dans le calcul
de stabilité linéaire de l'écoulement de base thermocapillaire par
Priede et Gerbeth (1997a). Ces auteurs ont de plus considéré la
présence de parois dans les directions  et
et 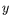 , ce qui leur a
permis de retrouver les rouleaux stationnaires (co-rotatifs) de
l'écoulement de base et surtout de déterminer le seuil de
l'instabilité globale en ondes hydrothermales. Nous reviendrons
plus en détail sur le caractère convectif, absolu et
global de l'instabilité dans le chapitre
, ce qui leur a
permis de retrouver les rouleaux stationnaires (co-rotatifs) de
l'écoulement de base et surtout de déterminer le seuil de
l'instabilité globale en ondes hydrothermales. Nous reviendrons
plus en détail sur le caractère convectif, absolu et
global de l'instabilité dans le chapitre ![[*]](crossref.png) .
Remarquons néanmoins que les calculs et distinctions faites par
Priede et Gerbeth (1997a) sont entièrement linéaires et obtenus après
intégrations itératives sur l'ensemble du plan des nombres d'ondes
complexes
.
Remarquons néanmoins que les calculs et distinctions faites par
Priede et Gerbeth (1997a) sont entièrement linéaires et obtenus après
intégrations itératives sur l'ensemble du plan des nombres d'ondes
complexes 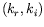 . Une description à partir d'équations
d'amplitude permet d'aller beaucoup plus loin, notamment jusqu'à une
distinction convectif/absolu non-linéaire. Nous nous référerons
dans ce cas aux travaux de Chomaz et Couairon (1999), Couairon et Chomaz (1999). Le chapitre
. Une description à partir d'équations
d'amplitude permet d'aller beaucoup plus loin, notamment jusqu'à une
distinction convectif/absolu non-linéaire. Nous nous référerons
dans ce cas aux travaux de Chomaz et Couairon (1999), Couairon et Chomaz (1999). Le chapitre
![[*]](crossref.png) est consacré à cette étude.
est consacré à cette étude.




suivant: 1.4 Une modélisation idoine
monter: 1.3 Analyse de stabilité
précédent: 1.3.5.4 Conclusion
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) .
Remarquons néanmoins que les calculs et distinctions faites par
Priede et Gerbeth (1997a) sont entièrement linéaires et obtenus après
intégrations itératives sur l'ensemble du plan des nombres d'ondes
complexes
.
Remarquons néanmoins que les calculs et distinctions faites par
Priede et Gerbeth (1997a) sont entièrement linéaires et obtenus après
intégrations itératives sur l'ensemble du plan des nombres d'ondes
complexes ![[*]](crossref.png) est consacré à cette étude.
est consacré à cette étude.