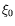et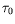 
, ni trop « longs ».
Néanmoins leur portée est très grande ; en effet, compte tenu de
leur universalité (seules les symétries du problème contraignent
la forme de l'équation), elles peuvent être appliquées à une
très grande diversité de systèmes.
Nous présentons en annexe ![[*]](crossref.png)
une extension possible de
l'équation d'amplitude de Ginzburg-Landau telle que les résultats
expérimentaux dans la cellule périodique unidimensionnelle (anneau)
la suggèrent ; a priori, cette nouvelle équation n'a pas un domaine
de validité plus étendu que celui de l'équation de départ mais
en tout cas, elle décrit bien les résultats expérimentaux sur une
grande plage de valeurs supercritiques de 
.
Une extension possible du domaine de validité peut être réalisée
par l'abandon de l'amplitude du mode le plus instable comme variable
pertinente, mais en autorisant plusieurs modes complets. Une telle
approche est par exemple celle des équations modèles, telles
celle de Swift et Hohenberg (1977) (SH) pour la convection de Rayleigh-Bénard.
Cette approche est plus simple que celle des équations constitutives,
et valide pour une plage de valeurs du paramètre de contrôle plus
grande que pour les équations d'amplitude. Elle a par exemple été
menée fructueusement dans le cas de l'optique non-linéaire où les
équations de Maxwell-Bloch ont été réduites à un modèle de
type SH par Lega et al. (1994). Malheureusement, il n'existe pas à l'heure
actuelle de tel modèle pour l'étude des ondes hydrothermales.