



suivant: 1.4.5.2 Mesures expérimentales
monter: 1.4.5 Quelques valeurs des
précédent: 1.4.5 Quelques valeurs des
Table des matières
Nous pouvons utiliser nos calculs de stabilité linéaire
(§ ![[*]](crossref.png) ) pour obtenir numériquement les valeurs
de quelques coefficients des équations d'amplitude.
) pour obtenir numériquement les valeurs
de quelques coefficients des équations d'amplitude.
Figure:
Exemple de courbes
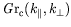 (à gauche) et
(à gauche) et
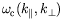 (à droite). Chaque point est obtenu
en fixant
(à droite). Chaque point est obtenu
en fixant
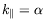 et
et
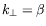 et en résolvant
(
et en résolvant
(![[*]](crossref.png) ). Chaque courbe est obtenue
en fixant
). Chaque courbe est obtenue
en fixant 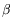 et en variant
et en variant 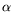 . Les valeurs des paramètres
ont été choisies ainsi :
. Les valeurs des paramètres
ont été choisies ainsi :
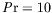 ,
, 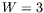 ,
,
 et courbure nulle.
et courbure nulle.
|
|
En effet, outre les valeurs du nombre de Marangoni critique, de la
fréquence critique 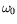 et du vecteur d'onde critique
et du vecteur d'onde critique
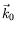 , nous avons plus généralement accès aux courbes
, nous avons plus généralement accès aux courbes
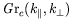 et
et
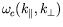 en
résolvant l'équation
caractéristique (
en
résolvant l'équation
caractéristique (![[*]](crossref.png) ) pour chaque couple
de composantes du nombre d'onde
) pour chaque couple
de composantes du nombre d'onde
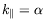 et
et
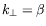 données. La figure
données. La figure ![[*]](crossref.png) présente de
telles courbes critiques. Comme noté par Laure et Mutabazi (1994), cela nous
permet d'en déduire :
ainsi que :
Ces dernières expressions sont reliées à notre définition du
paramètre de contrôle
présente de
telles courbes critiques. Comme noté par Laure et Mutabazi (1994), cela nous
permet d'en déduire :
ainsi que :
Ces dernières expressions sont reliées à notre définition du
paramètre de contrôle  :
En nous plaçant dans le cas sans courbure correspondant au
rectangle, pour une hauteur de fluide
:
En nous plaçant dans le cas sans courbure correspondant au
rectangle, pour une hauteur de fluide 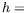 1,7 mm et une extension
1,7 mm et une extension
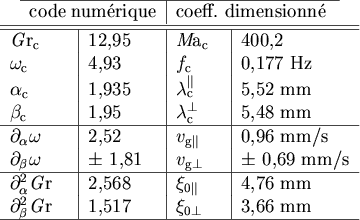
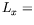 10 mm, nous trouvons alors un jeu de valeurs, que nous
re-dimensionalisons avec les échelles de temps
10 mm, nous trouvons alors un jeu de valeurs, que nous
re-dimensionalisons avec les échelles de temps 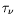 =4.44 s et
d'espace
=4.44 s et
d'espace 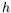 comme définies précédement. Le tableau de la
figure
comme définies précédement. Le tableau de la
figure ![[*]](crossref.png) présente les résultats
obtenus.
présente les résultats
obtenus.
Figure:
Valeurs numériques des parties réelles des coefficients
en facteur des termes linéaires de l'équation d'amplitude
au seuil des ondes hydrothermales pour
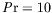 ,
, 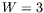 ,
,
 ,
courbure nulle.
,
courbure nulle.
 |
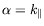 et
et
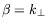 sont les composantes
du vecteur d'onde selon la direction du gradient et selon la direction
perpendiculaire. Le problème étant décomposé selon ces deux
directions, il nous est aisé de calculer les dérivées partielles
selon chacune d'entre elles.
sont les composantes
du vecteur d'onde selon la direction du gradient et selon la direction
perpendiculaire. Le problème étant décomposé selon ces deux
directions, il nous est aisé de calculer les dérivées partielles
selon chacune d'entre elles.
Remarquons au passage que nous observons
(figure ![[*]](crossref.png) ) une très faible courbure de
la surface
) une très faible courbure de
la surface
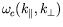 ; or cette courbure est
liée au coefficient
; or cette courbure est
liée au coefficient  (relation
(relation ![[*]](crossref.png) ) qui doit donc
être très petit (
) qui doit donc
être très petit (
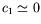 ).
).




suivant: 1.4.5.2 Mesures expérimentales
monter: 1.4.5 Quelques valeurs des
précédent: 1.4.5 Quelques valeurs des
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ) pour obtenir numériquement les valeurs
de quelques coefficients des équations d'amplitude.
) pour obtenir numériquement les valeurs
de quelques coefficients des équations d'amplitude.
![[*]](crossref.png) ) pour chaque couple
de composantes du nombre d'onde
) pour chaque couple
de composantes du nombre d'onde
![[*]](crossref.png) présente de
telles courbes critiques. Comme noté par Laure et Mutabazi (1994), cela nous
permet d'en déduire :
présente de
telles courbes critiques. Comme noté par Laure et Mutabazi (1994), cela nous
permet d'en déduire :
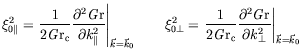
![[*]](crossref.png) présente les résultats
obtenus.
présente les résultats
obtenus.

![[*]](crossref.png) ) une très faible courbure de
la surface
) une très faible courbure de
la surface
![]() ; or cette courbure est
liée au coefficient
; or cette courbure est
liée au coefficient ![]() (relation
(relation ![[*]](crossref.png) ) qui doit donc
être très petit (
) qui doit donc
être très petit (
![]() ).
).