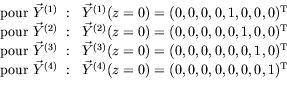suivant: 1.3.3 Instabilités stationnaires
monter: 1.3.2 Equations pour les
précédent: 1.3.2.1 Equations
Table des matières
Nous résolvons alors le problème en utilisant la méthode exposée
par Mercier (1997) et que nous résumons ci-dessous.
Nous nous plaçons à la limite de la stabilité marginale
(
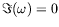 ) et recherchons une solution
) et recherchons une solution
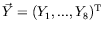 du système précédent sous la forme d'une
combinaison linéaire de quatre solutions linéairement
indépendantes, que nous notons
du système précédent sous la forme d'une
combinaison linéaire de quatre solutions linéairement
indépendantes, que nous notons
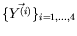 :
:
Chacune des quatre fonctions
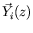 est obtenue en intégrant le
système (
est obtenue en intégrant le
système (![[*]](crossref.png) ) du premier ordre en
) du premier ordre en 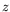 , avec les conditions
« initiales » suivantes en
, avec les conditions
« initiales » suivantes en 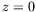 :
En satisfaisant ensuite les conditions limites en
:
En satisfaisant ensuite les conditions limites en 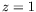 pour la
combinaison
pour la
combinaison
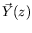 , l'on obtient un système algébrique
4
, l'on obtient un système algébrique
4 4 qui n'a de solution que si son déterminant s'annule. Cela
conduit à l'équation caractéristique suivante :
4 qui n'a de solution que si son déterminant s'annule. Cela
conduit à l'équation caractéristique suivante :
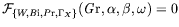 |
(1.10) |
Comme nous l'avons noté, 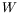 ,
,
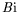 ,
,
 et
et 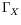 sont des
paramètres. Pour des raisons d'ordre pratique, nous traiterons les
deux composantes
sont des
paramètres. Pour des raisons d'ordre pratique, nous traiterons les
deux composantes 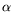 et
et 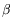 du vecteur d'onde comme des
paramètres. Il ne reste alors qu'à chercher le couple de valeurs de
du vecteur d'onde comme des
paramètres. Il ne reste alors qu'à chercher le couple de valeurs de
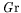 et
et 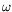 qui annule simultanément les parties réelle et
imaginaire de l'équation caractéristique. Si l'on recherche une
instabilité stationnaire, la partie imaginaire de l'équation est
automatiquement annulée en fixant
qui annule simultanément les parties réelle et
imaginaire de l'équation caractéristique. Si l'on recherche une
instabilité stationnaire, la partie imaginaire de l'équation est
automatiquement annulée en fixant 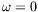 .
.
La mise en pratique de la méthode ci-dessus a été effectuée en
adaptant un code de Jean-François Mercier et Christiane Normand.




suivant: 1.3.3 Instabilités stationnaires
monter: 1.3.2 Equations pour les
précédent: 1.3.2.1 Equations
Table des matières
Nicolas Garnier - Thèse de doctorat
![]() ) et recherchons une solution
) et recherchons une solution
![]() du système précédent sous la forme d'une
combinaison linéaire de quatre solutions linéairement
indépendantes, que nous notons
du système précédent sous la forme d'une
combinaison linéaire de quatre solutions linéairement
indépendantes, que nous notons
![]() :
:
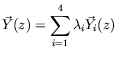
![[*]](crossref.png) ) du premier ordre en
) du premier ordre en