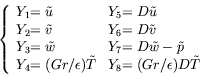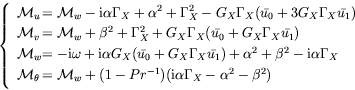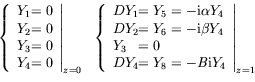suivant: 1.3.2.2 Méthode de résolution
monter: 1.3.2 Equations pour les
précédent: 1.3.2 Equations pour les
Table des matières
Après avoir injecté les expressions ci-dessus dans les
équations (![[*]](crossref.png) ), nous tronquons ces dernières à l'ordre
linéaire en les perturbations ; cela nous permet de prendre la
transformée de Fourier :
Seule subsiste alors une dépendance en
), nous tronquons ces dernières à l'ordre
linéaire en les perturbations ; cela nous permet de prendre la
transformée de Fourier :
Seule subsiste alors une dépendance en 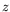 ; nous notons
; nous notons
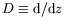 . Nous posons
. Nous posons
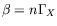 et définissons (pour des
raisons de simplicité d'écriture) les nouvelles variables
suivantes :
et :
Il vient ainsi le système suivant pour l'évolution des perturbations :
et définissons (pour des
raisons de simplicité d'écriture) les nouvelles variables
suivantes :
et :
Il vient ainsi le système suivant pour l'évolution des perturbations :
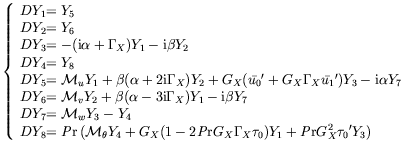 |
(1.9) |
A ces équations nous devons ajouter les conditions aux limites
adéquates pour les perturbations, qui sous leur forme adimensionnée
s'écrivent :
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ), nous tronquons ces dernières à l'ordre
linéaire en les perturbations ; cela nous permet de prendre la
transformée de Fourier :
), nous tronquons ces dernières à l'ordre
linéaire en les perturbations ; cela nous permet de prendre la
transformée de Fourier :