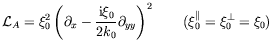suivant: Remarque sur l'ordre de
monter: 1.4 Une modélisation idoine
précédent: 1.4 Une modélisation idoine
Table des matières
1.4.1 Développement en échelles multiples et difficultés
Une analyse faiblement non-linéaire autour du seuil de l'instabilité
en ondes hydrothermales a été entreprise par Smith (1988) dans le
but de déterminer si les ondes hydrothermales étaient des ondes
propagatives couplées non-linéairement de façon destructive ou
au contraire couplées de sorte à donner des ondes stationnaires.
Cette approche classique consiste à effectuer un développement en
échelles multiples utilisant le petit paramètre
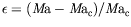 , distance au seuil
adimensionnée. Malheureusement, la résolution de la condition de
solvabilité, permettant de donner les équations d'amplitude
attendues, doit être effectuée par voie numérique. La structure de
ces équations peut néanmoins être écrite formellement et Smith
obtient1.5 :
, distance au seuil
adimensionnée. Malheureusement, la résolution de la condition de
solvabilité, permettant de donner les équations d'amplitude
attendues, doit être effectuée par voie numérique. La structure de
ces équations peut néanmoins être écrite formellement et Smith
obtient1.5 :
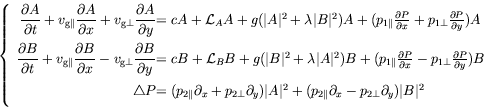
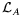 et
et
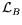 sont des opérateurs de dérivation
spatiale du second ordre explicités plus loin.
sont des opérateurs de dérivation
spatiale du second ordre explicités plus loin. 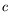 ,
,
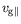 ,
,
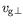 ,
, 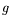 ,
,
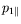 ,
,
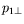 ,
,
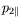 et
et
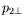 sont des coefficients
complexes qui dépendent du nombre de Prandtl et des conditions aux
limites et sont déterminés numériquement. L'existence de la
troisième équation n'est qu'un jeu d'écriture. En effet, cette
dernière relation entre
sont des coefficients
complexes qui dépendent du nombre de Prandtl et des conditions aux
limites et sont déterminés numériquement. L'existence de la
troisième équation n'est qu'un jeu d'écriture. En effet, cette
dernière relation entre 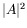 ,
, 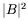 , et
, et 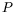 est linéaire et
peut être inversée de sorte à éliminer
est linéaire et
peut être inversée de sorte à éliminer 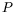 des deux premières
équations. Formellement :
des deux premières
équations. Formellement :
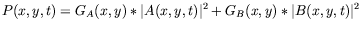
où 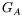 et
et 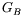 sont les fonctions de Green suivantes :
sont les fonctions de Green suivantes :
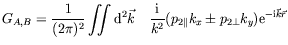
Ceci fait apparaître deux termes intégraux dans chacune des deux
équations pour 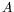 et
et 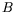 . Ces termes traduisent l'existence d'un
écoulement à grande échelle. Dans la suite, nous négligeons ces
termes.
. Ces termes traduisent l'existence d'un
écoulement à grande échelle. Dans la suite, nous négligeons ces
termes.
Notons que
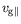 désigne la vitesse de groupe dans
la direction
désigne la vitesse de groupe dans
la direction  du gradient de température et
du gradient de température et
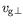 la vitesse de groupe dans la direction
la vitesse de groupe dans la direction 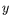 orthogonale au gradient. Le changement de signe de la vitesse de groupe
entre l'équation pour
orthogonale au gradient. Le changement de signe de la vitesse de groupe
entre l'équation pour 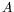 et celle pour
et celle pour 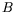 n'est opéré que sur
n'est opéré que sur
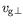 ce qui traduit un fait observé dans les
expériences : les ondes se propagent toujours du froid vers le chaud
dans la direction
ce qui traduit un fait observé dans les
expériences : les ondes se propagent toujours du froid vers le chaud
dans la direction  , mais choisissent entre la droite et la gauche
dans la direction
, mais choisissent entre la droite et la gauche
dans la direction 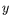 . Cette différence entre les directions
. Cette différence entre les directions  et
et
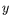 n'est rien d'autre que la signature de la brisure de symétrie par
le gradient de température, brisure imposée sur l'écoulement de
base, avant la bifurcation. Les opérateurs de dérivation spatiale
n'est rien d'autre que la signature de la brisure de symétrie par
le gradient de température, brisure imposée sur l'écoulement de
base, avant la bifurcation. Les opérateurs de dérivation spatiale
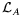 et
et
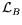 , ainsi que ceux affectés des coefficients
, ainsi que ceux affectés des coefficients
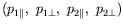 sur les
termes de pression gardent eux aussi la trace de cette
« dissymétrie ».
sur les
termes de pression gardent eux aussi la trace de cette
« dissymétrie ».
Nous avons :
où les coefficients sont a priori complexes.
Nous observons ainsi que la symétrie droite/gauche est préservée :
La structure de ces termes spatiaux est identique à celle des
équations de Ginzburg-Landau complexe (
 GL) pour les milieux
excitables isotropes ainsi qu'à celle de l'équation de
Ginzburg-Pitaevskii pour les fluides anisotropes. Dans le cas de
GL) pour les milieux
excitables isotropes ainsi qu'à celle de l'équation de
Ginzburg-Pitaevskii pour les fluides anisotropes. Dans le cas de
 GL :
GL :
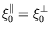
et
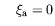
et dans le cas de Ginzburg-Pitaevskii :
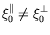
et
La structure du terme spatial trouvé par Smith -- et qui est aussi
celui de toutes les équations précédentes -- est différente de
la structure du terme spatial de l'équation de NWS déduite par
Segel (1969), Newell et Whitehead (1969) pour une structure stationnaire de
convection de Rayleigh-Bénard dans un milieu isotrope :
Les différences entre tous ces termes trouvent leur origine dans les
symétries spatiales du problème considéré. Le cas des ondes
hydrothermales correspond à celui d'une géométrie anisotrope : la
direction du gradient de température n'a pas le même rôle que la
direction perpendiculaire. La symétrie
 n'existe en
effet pas ; cela conditionne le choix a priori des termes spatiaux qui
ont un sens. Nous allons dans les sections suivantes reconstruire les
équations d'amplitude à partir des symétries.
n'existe en
effet pas ; cela conditionne le choix a priori des termes spatiaux qui
ont un sens. Nous allons dans les sections suivantes reconstruire les
équations d'amplitude à partir des symétries.
Sous-sections




suivant: Remarque sur l'ordre de
monter: 1.4 Une modélisation idoine
précédent: 1.4 Une modélisation idoine
Table des matières
Nicolas Garnier - Thèse de doctorat
![]() , distance au seuil
adimensionnée. Malheureusement, la résolution de la condition de
solvabilité, permettant de donner les équations d'amplitude
attendues, doit être effectuée par voie numérique. La structure de
ces équations peut néanmoins être écrite formellement et Smith
obtient1.5 :
, distance au seuil
adimensionnée. Malheureusement, la résolution de la condition de
solvabilité, permettant de donner les équations d'amplitude
attendues, doit être effectuée par voie numérique. La structure de
ces équations peut néanmoins être écrite formellement et Smith
obtient1.5 :
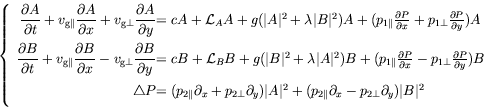
![]() désigne la vitesse de groupe dans
la direction
désigne la vitesse de groupe dans
la direction ![]() du gradient de température et
du gradient de température et
![]() la vitesse de groupe dans la direction
la vitesse de groupe dans la direction ![]() orthogonale au gradient. Le changement de signe de la vitesse de groupe
entre l'équation pour
orthogonale au gradient. Le changement de signe de la vitesse de groupe
entre l'équation pour ![]() et celle pour
et celle pour ![]() n'est opéré que sur
n'est opéré que sur
![]() ce qui traduit un fait observé dans les
expériences : les ondes se propagent toujours du froid vers le chaud
dans la direction
ce qui traduit un fait observé dans les
expériences : les ondes se propagent toujours du froid vers le chaud
dans la direction ![]() , mais choisissent entre la droite et la gauche
dans la direction
, mais choisissent entre la droite et la gauche
dans la direction ![]() . Cette différence entre les directions
. Cette différence entre les directions ![]() et
et
![]() n'est rien d'autre que la signature de la brisure de symétrie par
le gradient de température, brisure imposée sur l'écoulement de
base, avant la bifurcation. Les opérateurs de dérivation spatiale
n'est rien d'autre que la signature de la brisure de symétrie par
le gradient de température, brisure imposée sur l'écoulement de
base, avant la bifurcation. Les opérateurs de dérivation spatiale
![]() et
et
![]() , ainsi que ceux affectés des coefficients
, ainsi que ceux affectés des coefficients
![]() sur les
termes de pression gardent eux aussi la trace de cette
« dissymétrie ».
sur les
termes de pression gardent eux aussi la trace de cette
« dissymétrie ».
![]() GL) pour les milieux
excitables isotropes ainsi qu'à celle de l'équation de
Ginzburg-Pitaevskii pour les fluides anisotropes. Dans le cas de
GL) pour les milieux
excitables isotropes ainsi qu'à celle de l'équation de
Ginzburg-Pitaevskii pour les fluides anisotropes. Dans le cas de
![]() GL :
GL :