



suivant: 3.1.1.2.1 - Conditions limites
monter: 3.1.1 Cas de l'équation
précédent: 3.1.1.1.6 Conditions limites finies
Table des matières
Les solutions non-triviales de
 GL mises en avant dans le paragraphe
précédent correspondent dans l'espace réel à des ondes. La
solution triviale
GL mises en avant dans le paragraphe
précédent correspondent dans l'espace réel à des ondes. La
solution triviale 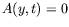 correspond quant à elle à l'état de
base, où plus précisément à l'absence d'ondes dans le formalisme
des équations d'amplitudes ; nous l'appellons état de repos.
Nous allons maintenant chercher les conditions de stabilité de cette
solution. Gardons néanmoins présent à l'esprit que si cette
dernière se déstabilise, c'est pour former une solution non-triviale
telle que celles énoncées précédemment ; de plus, la stabilité
linéaire de l'état de repos est donnée par le taux de croissance
d'une perturbation ajoutée à la solution
correspond quant à elle à l'état de
base, où plus précisément à l'absence d'ondes dans le formalisme
des équations d'amplitudes ; nous l'appellons état de repos.
Nous allons maintenant chercher les conditions de stabilité de cette
solution. Gardons néanmoins présent à l'esprit que si cette
dernière se déstabilise, c'est pour former une solution non-triviale
telle que celles énoncées précédemment ; de plus, la stabilité
linéaire de l'état de repos est donnée par le taux de croissance
d'une perturbation ajoutée à la solution 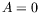 , c'est à dire d'une
solution de l'équation
, c'est à dire d'une
solution de l'équation
 GL linéarisée que nous avons déjà
résolue. La fréquence doit dorénavant être complexe, mais elle
satisfait la même relation de dispersion (
GL linéarisée que nous avons déjà
résolue. La fréquence doit dorénavant être complexe, mais elle
satisfait la même relation de dispersion (![[*]](crossref.png) ).
).
Sous-sections
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ).
).