



suivant: 3.1.1.1 Forme des solutions
monter: 3.1 Instabilité primaire en
précédent: 3.1 Instabilité primaire en
Table des matières
3.1.1 Cas de l'équation de Ginzburg-Landau complexe
L'équation d'amplitude que nous utilisons a été introduite
en § ![[*]](crossref.png) dans le cas de deux ondes contra-propagatives.
Ici, pour des raisons de simplicité, nous ne nous intéressons qu'au
cas d'une onde unique, que nous supposons être (par exemple) une onde
droite dont l'amplitude
dans le cas de deux ondes contra-propagatives.
Ici, pour des raisons de simplicité, nous ne nous intéressons qu'au
cas d'une onde unique, que nous supposons être (par exemple) une onde
droite dont l'amplitude 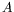 vérifie :
vérifie :
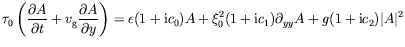 |
(3.1) |
Deissler (1985) a le premier étudié l'effet de la vitesse de
groupe 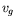 vue comme une vitesse d'advection dans le cas d'un
écoulement sans advection extérieure imposée. C'est tout
naturellement qu'il a utilisé une équation modèle du type
vue comme une vitesse d'advection dans le cas d'un
écoulement sans advection extérieure imposée. C'est tout
naturellement qu'il a utilisé une équation modèle du type
 GL
avec le terme
GL
avec le terme
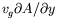 . L'origine de ce terme
n'importe pas ; son interprétation étant -- de façon
équivalente -- soit la présence d'une advection moyenne forcée
par l'extérieur (écoulement moyen, exemple : un sillage avec une
vitesse
. L'origine de ce terme
n'importe pas ; son interprétation étant -- de façon
équivalente -- soit la présence d'une advection moyenne forcée
par l'extérieur (écoulement moyen, exemple : un sillage avec une
vitesse 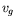 ), soit l'existence d'une vitesse de groupe (dans le cas
d'une instabilité en ondes propagatives). Nous nous restreignons dans
toute la suite au cas où
), soit l'existence d'une vitesse de groupe (dans le cas
d'une instabilité en ondes propagatives). Nous nous restreignons dans
toute la suite au cas où 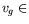 IR ; le cas complémentaire
IR ; le cas complémentaire
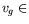 iIR a été étudié par Rovinsky et al. (1996) comme
résultant d'un écoulement différentiel.
iIR a été étudié par Rovinsky et al. (1996) comme
résultant d'un écoulement différentiel.
L'existence de  et
et 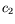 complique un peu la dynamique par rapport
au cas d'une instabilité stationnaire décrite par une équation de
Ginzburg-Landau réelle (IRGL). Les calculs pour le premier seuil
sont cependant encore très simples ; nous les reproduisons ici dans un
contexte un peu différent de celui des articles originaux de
Deissler (1987), Deissler (1989), Deissler (1985), en insistant comme
Tobias et al. (1998) sur l'effet de la géométrie finie.
complique un peu la dynamique par rapport
au cas d'une instabilité stationnaire décrite par une équation de
Ginzburg-Landau réelle (IRGL). Les calculs pour le premier seuil
sont cependant encore très simples ; nous les reproduisons ici dans un
contexte un peu différent de celui des articles originaux de
Deissler (1987), Deissler (1989), Deissler (1985), en insistant comme
Tobias et al. (1998) sur l'effet de la géométrie finie.
Comme nous l'avons déjà suggéré, la distinction entre
instabilité convective et absolue a un sens dans le cas d'une
boîte finie, mais pas en géométrie périodique. La
spécification des conditions aux limites est un point crucial de
l'analyse du problème.
Sous-sections




suivant: 3.1.1.1 Forme des solutions
monter: 3.1 Instabilité primaire en
précédent: 3.1 Instabilité primaire en
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) dans le cas de deux ondes contra-propagatives.
Ici, pour des raisons de simplicité, nous ne nous intéressons qu'au
cas d'une onde unique, que nous supposons être (par exemple) une onde
droite dont l'amplitude
dans le cas de deux ondes contra-propagatives.
Ici, pour des raisons de simplicité, nous ne nous intéressons qu'au
cas d'une onde unique, que nous supposons être (par exemple) une onde
droite dont l'amplitude ![]() et
et ![]() complique un peu la dynamique par rapport
au cas d'une instabilité stationnaire décrite par une équation de
Ginzburg-Landau réelle (IRGL). Les calculs pour le premier seuil
sont cependant encore très simples ; nous les reproduisons ici dans un
contexte un peu différent de celui des articles originaux de
Deissler (1987), Deissler (1989), Deissler (1985), en insistant comme
Tobias et al. (1998) sur l'effet de la géométrie finie.
complique un peu la dynamique par rapport
au cas d'une instabilité stationnaire décrite par une équation de
Ginzburg-Landau réelle (IRGL). Les calculs pour le premier seuil
sont cependant encore très simples ; nous les reproduisons ici dans un
contexte un peu différent de celui des articles originaux de
Deissler (1987), Deissler (1989), Deissler (1985), en insistant comme
Tobias et al. (1998) sur l'effet de la géométrie finie.