2.3.2.2 Résolution

Nous proposons ci-dessous la résolution de l'équation « maîtresse » () dans quelques cas qui nous intéressent particulièrement : régime conductif de Rayleigh-Bénard, écoulement de base thermocapillaire, et perturbations par des ondes de température.

$\bullet$ Dans le cas où l'indice ne dépend que de $z$, et avec les conditions aux limites énoncées :

$$\Rightarrow \quad \frac{d}{dz}(nx') = 0 \quad \Rightarrow \quad nx' = 0 \quad \Rightarrow \quad x = x_0$$

Le rayon est donc purement vertical. Ce cas correspond par exemple à un indice $n$ constant (fluide au repos) ou au régime conductif de Rayleigh-Bénard. Une dépendance purement verticale de la température n'a donc pas d'influence sur le faisceau ; ce n'est plus le cas lorsqu'une dépendance horizontale est présente.

$\bullet$ Dans le cas où l'indice dépend de $z$ et $x$, mais où cette dépendance est séparable sous la forme d'une somme :

$$n(x,z) = n_0 + n_1 x + n_2(z) \quad n_1 x \ll n_0 \quad \forall x \in [0, L_x]$$

$$\quad \left\vert n_2(z)\right\vert \ll n_0 \quad \forall z \in [0,h]$$

Une telle écriture correspond comme nous allons le voir au cas de l'écoulement de base thermocapillaire en géométrie rectangulaire (§ , éq. ()). Nous résolvons alors l'équation à l'ordre le plus bas en $(hn_1/n_0)$ :

$$\Rightarrow \quad \frac{d}{dz}(nx') = n_1 \quad \Rightarrow \quad nx' = n_1 z \quad \Rightarrow \quad x = x_0 + \frac{n_1}{2 n_0} z^2$$

Etant donnée la forme du profil de température dans l'écoulement de base en géométrie rectangulaire, on peut écrire :

$$n(x,z) = n_0 + \frac{\mathrm dn}{\mathrm dT}\left(\frac{\partial T}{\partial x}(x-x^*) + \frac{\partial T}{\partial z}(z-z^*) \right)$$

$$\doteq n_0 + n_1 x + n_2(z)$$

$$\Rightarrow~ n_1 = \frac{\mathrm dn}{\mathrm dT} \beta$$

où $\beta$ est le gradient horizontal de température $\Delta T/L_x$. La direction ici notée $x$ correspond à la direction notée $x$ pour l'écoulement de base. La dépendance très simple en $x$ de l'écoulement de base permet d'avoir un résultat indépendant de la dépendance en $z$, tout comme dans le cas d'un indice seulement variable avec $z$. Cette propriété cesse d'être vraie pour un écoulement de base perturbé par les ondes hydrothermales, mais nous négligerons dans ce cas la dépendance en $z$ de $n$, car celle-ci n'a qu'une influence réduite sur la déviation du faisceau ; cela est de plus corroboré par le fait que nous intégrons $z$ sur l'épaisseur de la couche de fluide.

$n_1$ et $n_2(z)$ sont proportionnels à $\vert dn/dT \Delta T\vert \ll 1$, ce qui justifie les approximations faites a priori sur l'expression de $n$. Comme $dn/dT<0$ pour les fluides, on en déduit que l'image sera uniformément déviée du côté froid (cf. $\beta(x-x_0)<0$). Cette déviation n'aura aucune influence sur nos mesures car elle ne provoque qu'une translation de l'image.

Dans le cas d'une cellule cylindrique, la translation $x-x_0$ se trouve affectée d'une dépendance en $\Phi(X) = {\phi}/{(1+\phi X)}$, tout comme les profils correspondants de l'écoulement de base (cf. § , formules ()). Nous supposons cet effet faible ; cela est justifié par l'allure des profils radiaux de température présentés en § . Dans le cas de la cellule « disque », nous pouvons donc prédire a priori un agrandissement de l'image lorsque le chauffage a lieu au centre ( $\Delta T < 0$, rayons lumineux défléchis vers l'extérieur), et une réduction de l'image lorsque le centre est plus froid ( $\Delta T > 0$, rayons défléchis vers le centre).

Notre calcul omet cependant la variation de hauteur induite par les effets thermocapillaires et exposée en §  (formule ()). Bien que cette dernière soit faible, elle est assez importante pour transformer la surface du fluide en un dioptre convergent si $\Delta T < 0$ (épaisseur d'huile plus petite au centre chaud) ou divergent si $\Delta T > 0$ (épaisseur d'huile plus grande au centre froid). La déviation globale du faisceau lumineux est alors essentiellement due à cet effet de surface, qui est de sens contraire à l'effet prédit par le calcul précédent sur les variations d'indice. Ainsi, les images obtenues pour $\Delta T > 0$ sont légèrement dilatées et le plot central apparaît plus grand ; de même, les images obtenues pour $\Delta T < 0$ sont légèrement contractées et le plot central apparaît plus petit. Ce phénomène est effectivement observé dans les expériences comme l'illustrent les clichés de la cellule « LOTUS » des chapitres  et . Notons que par un réglage approprié du dispositif optique expérimental, il est possible d'atténuer dans certaines limites cet effet.

$\bullet$ Dans le cas où l'indice est modulé par une perturbation monochromatique dans la direction $x$ (direction horizontale quelconque, qui ne coïncide plus nécessairement avec la direction du gradient), nous écrirons :

$$n(x) = n_0 + n_1 \cos(kx)$$   avec$$\quad n_0 \gg n_1$$

avec les mêmes conditions aux limites que précédemment ; il vient alors :

$$x'' + \frac{n_1}{n_0}k \sin(kx) = 0$$

qui est l'équation d'un oscillateur du type pendule pesant (!) où $z$ joue le rôle du temps. Nous intégrons une fois cette équation et nous en déduisons :

$$\Rightarrow (x')^2 = 2 \frac{n_1}{n_0} \left( \cos(kx) - \cos(kx_0) \right)$$

$$= 2 \frac{n_1}{n_0} \sin(k(x+x_0)/2) \sin(k(x_0-x)/2)$$

$$\simeq \frac{n_1}{n_0} \sin(k x_0) k (x_0-x)$$

où l'on a utilisé l'hypothèse selon laquelle $n_1 \ll n_0$ et donc que $\vert x'\vert \rightarrow 0$ et qu'ainsi $x-x_0 \rightarrow 0$ (ceci est l'hypothèse des faibles déviations... dans le cas du pendule pesant). Les expressions ci-dessus requièrent que le membre de droite soit positif. Cela peut être interprété comme suit (figure ) :

$kx_0 \in [0, \pi/2]$	$\Leftrightarrow$	$\sin(kx_0) > 0 \Rightarrow x>x_0$	et $\cos(kx_0) > 0 \quad \Rightarrow n(x)$ max.	(4)
$kx_0 \in [\pi/2, \pi]$	$\Leftrightarrow$	$\sin(kx_0) > 0 \Rightarrow x>x_0$	et $\cos(kx_0) < 0 \quad \Rightarrow n(x)$ min.	(3)
$kx_0 \in [-\pi,-\pi/2]$	$\Leftrightarrow$	$\sin(kx_0) < 0 \Rightarrow x<x_0$	et $\cos(kx_0) < 0 \quad \Rightarrow n(x)$ min.	(2)
$kx_0 \in [-\pi/2, 0]$	$\Leftrightarrow$	$\sin(kx_0) < 0 \Rightarrow x<x_0$	et $\cos(kx_0) > 0 \quad \Rightarrow n(x)$ max.	(1)

Figure: Illustration de l'effet lentille sur une période spatiale pour le cas simple d'une modulation monochromatique de l'indice. Les zones (1)-(4) se réfèrent aux phases de $kx_0$ évoquées dans le texte. Les rayons lumineux à l'intérieur du fluide sont des arcs de paraboles.

on écrira donc suivant les cas :

$$\displaystyle \frac{\mathrm dx}{\mathrm dz} = \pm \sqrt{\frac{2n_1k}{n_0}\vert\sin(kx_0)\vert} \sqrt{\vert x-x_0\vert}$$

ce qui, compte tenu de la condition $x=x_0$ en $z=0$, s'intègre et donne dans tous les cas :

$$x-x_0 = -\frac{n_1 k}{2 n_0} \sin(kx_0) z^2$$

Les rayons lumineux dans la couche de fluide sont donc des arcs de parabole. Nous pouvons calculer l'angle d'incidence sur la paroi inférieure de la cellule et en déduire par la loi de la réfraction de Descartes l'angle de sortie du rayon lumineux arrivé initialement en $x=x_0$ sur la surface libre :

$$\sin(i_{\text{sortie}}) = n \sin(i(z=h))$$

$$\simeq n_0 x'(z=h)$$

$$- \simeq n_1 k h \sin(kx_0)$$

Comme nous sommes en optique incohérente, nous pouvons écrire l'intensité lumineuse $I(x)$ reçue sur un écran horizontal situé à une distance $D$ de la paroi inférieure connaissant $I_0$ l'intensité du faisceau uniforme incident :

$$I(x) = \int_{} I_0 ~\delta(x_2-x) dx_0$$

avec :

$$x_2 - x_1 = - D \tan(i_{\text{sortie}})$$

$$x_1 - x_0 = - \frac{kn_1}{2n_0} \sin(kx_0) h^2$$

$$\Rightarrow x_2 - x_0 = - n_1 h k(D + \frac{h}{2n_0})\sin(kx_0)$$

$$\simeq - n_1 h k D \sin(kx_0) \quad D \gg h$$

On en déduit une expression de la distance focale équivalente ($+f_T$) au voisinage d'un maximum d'indice ( $kx_0 \simeq 0 [2\pi]$), i.e., d'une lentille locale convergente. Une zone de minimum d'indice ( $kx_0 \simeq \pi [2\pi]$) se comportera, elle, comme une lentille locale divergente de focale ($-f_T$). L'annulation de $\partial x_2 / \partial x_0$ (tous les rayons arrivent au foyer image) donne dans les deux cas :

$$f_T = \frac{h}{n_1 (hk)^2}$$ (2.2)

Si $D \ll f_T$, la relation entre $x_0$ et $x_2$ est bijective et dans la limite des déflections faibles, on obtient finalement pour expression de l'intensité le long de l'écran :

$$I(x) \simeq I_0 \left(1 + \frac{D}{f_T} \cos(k x) + ...\right)$$ (2.3)

Les points de suspension représentent les termes suivants du développement limité en $D/f_T$ qui sont en fait les harmoniques spatiaux ; la présence de ces derniers signale alors une déformation du signal. Cette déformation peut être intéressante si l'on veut des images bien contrastées, mais si l'on désire plutôt une information quantitative, il faut s'arranger pour réduire l'importance des harmoniques spatiaux, par exemple en se plaçant très en avant du plan focal ($D \ll f_T$).

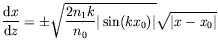
Nous relions enfin la variation d'indice aux variations de la température, afin de traduire l'influence des ondes de perturbation de température :

$$n(x) = n_0 + \frac{\mathrm dn}{\mathrm dT} \frac{\partial T}{\partial x} = n_0 + \frac{\mathrm dn}{\mathrm dT} \eta \cos(kx)$$

$$= n_0 + n_1 \cos(kx)$$

$$\Rightarrow n_1 = \frac{\mathrm dn}{\mathrm dT} \eta$$

où $\eta$ est l'amplitude des perturbations de température que l'on étudie^2.4 et $\mathrm dn/\mathrm dT<0$.

Remarque : Ce calcul peut être étendu au cas où $T(x)$ n'est plus sinusoïdale, mais quelconque : il suffit de décomposer $T$ en série de Fourier. A chaque mode $k$ de la série correspond alors une distance focale $f_T(k)$. En utilisant la passerelle $\{$   i$k \leftrightarrow \partial/\partial x \leftrightarrow \vec{\nabla} \}$, nous en déduisons :

$$I(x) \simeq I_0 \left( 1 + D h \frac{\mathrm dn}{\mathrm dT} (\vec{\nabla})^2 T + ... \right)$$

Les termes suivants peuvent être obtenus en développant aux ordres suivant l'intégrande, mais le premier ordre nous suffit car -- comme dans le cas de la convection de Rayleigh-Bénard -- les perturbations de température sont (quasi-)sinusoïdales au seuil de l'instabilité.

Commentaires : La réponse du système ombroscopique est dite « linéaire » si une perturbation monochromatique du champ de température (comme cela est le cas au seuil de l'instabilité) est signalée par une modulation monochromatique de l'intensité sur l'écran. Ce régime « linéaire » signifie que le montage optique ne réalise pas de distorsions -- ce qui se traduirait par l'apparition d'harmoniques -- et que le signal récupéré sur l'écran est quantitativement relié au champ de température via la formule (). Ce régime, que nous recherchons expérimentalement, nécessite que $D \ll f_T$, donc que le contraste ne soit pas trop fort. Notamment, lorsque nous nous éloignerons du seuil de l'instabilité, il faudra être attentif à l'augmentation de $n_1$, i.e. à la réduction de la distance focale. On peut de même remarquer que l'amplitude de la modulation de l'intensité dépend de la distance $D$, qu'il faudra donc maintenir constante lors d'une série d'expériences visant à mesurer et comparer des amplitudes d'ondes.