



suivant: 2.3.2.2 Résolution
monter: 2.3.2 Quantifications
précédent: 2.3.2 Quantifications
Table des matières
Le chemin 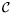 suivi par un rayon lumineux minimise le chemin
optique
suivi par un rayon lumineux minimise le chemin
optique 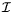 (principe de Fermat) :
Ce qui peut être réécrit sous la forme locale suivante :
(principe de Fermat) :
Ce qui peut être réécrit sous la forme locale suivante :
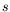 est l'abscisse curviligne et
est l'abscisse curviligne et 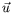 le vecteur unitaire tangent
au rayon lumineux. Plaçons nous dans un plan
le vecteur unitaire tangent
au rayon lumineux. Plaçons nous dans un plan 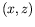 où
où  représente la direction horizontale dans laquelle les ondes se
développent et
représente la direction horizontale dans laquelle les ondes se
développent et 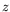 est orienté dans le sens des rayons parallèles
incidents (de bas en haut en pratique), et choisissons
est orienté dans le sens des rayons parallèles
incidents (de bas en haut en pratique), et choisissons 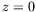 au niveau
du premier contact des rayons et du fluide (à la surface libre). Nous
avons alors deux équations scalaires entre lesquelles nous pouvons
éliminer l'abscisse curviligne
au niveau
du premier contact des rayons et du fluide (à la surface libre). Nous
avons alors deux équations scalaires entre lesquelles nous pouvons
éliminer l'abscisse curviligne 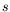 en nous plaçant dans la limite
des faibles déflections
en nous plaçant dans la limite
des faibles déflections
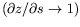 , ce
qui donne :
, ce
qui donne :
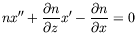 |
(2.1) |
où les primes dénotent la dérivation par rapport à 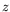 de la
trajectoire
de la
trajectoire 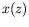 . Si l'on note
. Si l'on note 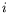 l'angle local du rayon par rapport
à la verticale, alors la limite des faibles déflections que nous
avons déjà invoquée s'écrit :
l'angle local du rayon par rapport
à la verticale, alors la limite des faibles déflections que nous
avons déjà invoquée s'écrit : 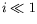 , i.e. :
L'équation « maîtresse » (
, i.e. :
L'équation « maîtresse » (![[*]](crossref.png) ) est du second
ordre. Les deux constantes d'intégration peuvent être fixées
simplement en imposant la position et l'angle d'impact d'un rayon
lumineux sur la surface libre en
) est du second
ordre. Les deux constantes d'intégration peuvent être fixées
simplement en imposant la position et l'angle d'impact d'un rayon
lumineux sur la surface libre en 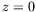 . Nous choisirons ainsi dans toute
la suite
. Nous choisirons ainsi dans toute
la suite 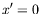 (incidence purement verticale) et
(incidence purement verticale) et 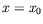 (abscisse du
point d'impact fixée).
(abscisse du
point d'impact fixée).




suivant: 2.3.2.2 Résolution
monter: 2.3.2 Quantifications
précédent: 2.3.2 Quantifications
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ) est du second
ordre. Les deux constantes d'intégration peuvent être fixées
simplement en imposant la position et l'angle d'impact d'un rayon
lumineux sur la surface libre en
) est du second
ordre. Les deux constantes d'intégration peuvent être fixées
simplement en imposant la position et l'angle d'impact d'un rayon
lumineux sur la surface libre en