



suivant: 2.3.4 Autres effets
monter: 2.3 Méthode d'observation par
précédent: 2.3.2.2 Résolution
Table des matières
2.3.3 Quantification des effets de surface
L'ombroscopie est évidemment sensible aux déflections de la surface
libre que nous avons jusqu'ici négligées. Il est ainsi possible de
détecter des ondes de surfaces, telles que les ondes de gravité
produites par un expérimentateur tremblotant en contact de la cellule
de convection, une pelleteuse voisine, ou bien la variation de hauteur
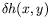 produite par les ondes hydrothermales. Supposons que la
surface soit faiblement déformée par les ondes suivant la relation :
produite par les ondes hydrothermales. Supposons que la
surface soit faiblement déformée par les ondes suivant la relation :
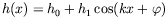
avec
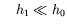
où 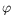 est une constante traduisant l'éventuel déphasage
entre
est une constante traduisant l'éventuel déphasage
entre 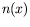 et
et 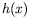 . Alors un calcul tout à fait analogue au
précédent conduit à l'obtention d'une distance focale traduisant
les effets de déformations de surface :
et à la formulation suivante de la modulation de l'intensité
reçue par l'écran :
De précédents travaux (F. Daviaud et J. Burguete) ont mesuré
l'amplitude des déflections de surface par les ondes
hydrothermales à l'aide d'un faisceau laser en incidence normale :
nous pouvons les chiffrer comme étant au plus de
. Alors un calcul tout à fait analogue au
précédent conduit à l'obtention d'une distance focale traduisant
les effets de déformations de surface :
et à la formulation suivante de la modulation de l'intensité
reçue par l'écran :
De précédents travaux (F. Daviaud et J. Burguete) ont mesuré
l'amplitude des déflections de surface par les ondes
hydrothermales à l'aide d'un faisceau laser en incidence normale :
nous pouvons les chiffrer comme étant au plus de 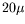 m. De plus,
Jenkins (1988) donne
m. De plus,
Jenkins (1988) donne
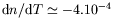 K
K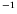 pour
les huiles de silicones2.5. Nous
pouvons donc comparer les effets de
pour
les huiles de silicones2.5. Nous
pouvons donc comparer les effets de 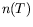 et de
et de 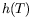 par le rapport :
Si -- comme nous l'avons écrit ci-dessus -- nous supposons que les
ondes de déflection de surface proviennent des ondes de température
dans le volume, nous pouvons utiliser la
relation (
par le rapport :
Si -- comme nous l'avons écrit ci-dessus -- nous supposons que les
ondes de déflection de surface proviennent des ondes de température
dans le volume, nous pouvons utiliser la
relation (![[*]](crossref.png) ) et nous obtenons alors un rapport de
l'ordre de 100, ce qui semble surestimé. En effet, si des
déflections de surface existent au niveau des ondes, leur amplitude
n'a aucune raison d'être reliée à l'amplitude de l'onde de
température -- au contraire de l'écoulement de base -- ; de plus,
le déphasage
) et nous obtenons alors un rapport de
l'ordre de 100, ce qui semble surestimé. En effet, si des
déflections de surface existent au niveau des ondes, leur amplitude
n'a aucune raison d'être reliée à l'amplitude de l'onde de
température -- au contraire de l'écoulement de base -- ; de plus,
le déphasage 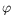 peut éventuellement amortir l'ensemble de la
déflection.
peut éventuellement amortir l'ensemble de la
déflection.
Quoi qu'il en soit, nous pouvons dans toute la suite considérer
l'équivalence entre amplitude du signal ombroscopique et amplitude des
ondes hydrothermales à condition de positionner l'écran à une
distance 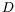 petite devant
petite devant 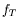 et
et 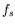 .
.




suivant: 2.3.4 Autres effets
monter: 2.3 Méthode d'observation par
précédent: 2.3.2.2 Résolution
Table des matières
Nicolas Garnier - Thèse de doctorat
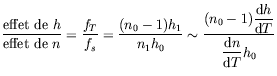
![[*]](crossref.png) ) et nous obtenons alors un rapport de
l'ordre de 100, ce qui semble surestimé. En effet, si des
déflections de surface existent au niveau des ondes, leur amplitude
n'a aucune raison d'être reliée à l'amplitude de l'onde de
température -- au contraire de l'écoulement de base -- ; de plus,
le déphasage
) et nous obtenons alors un rapport de
l'ordre de 100, ce qui semble surestimé. En effet, si des
déflections de surface existent au niveau des ondes, leur amplitude
n'a aucune raison d'être reliée à l'amplitude de l'onde de
température -- au contraire de l'écoulement de base -- ; de plus,
le déphasage ![]() petite devant
petite devant ![]() et
et ![]() .
.