next up previous contents
suivant: 3.1.4.3 Coefficients de réflexion monter: 3.1.4 Discussion précédent: 3.1.4.1 Formalisme convectif/absolu pour   Table des matières


3.1.4.2 Transition linéaire ou non-linéaire

La figure [*] illustre un état linéairement stable, convectivement instable et absolument instable ; cela correspond aux calculs développés en § [*] sur l'équation de Ginzburg-Landau linéarisée : seules des perturbations infiniment faibles sont considérées. Chomaz (1992), Couairon et Chomaz (1999) ont posé et résolu la question de la transition convectif/absolu non-linéaire ; les états correspondants sont illustrés sur la figure [*]. C'est la vitesse du front arrière qui pilote l'advection de la perturbation non-linéaire en lieu et place de la vitesse de groupe.

Figure: Représentations schématiques d'une perturbation non-linéairement convectivement instable et non-linéairement absolument instable en géométrie infinie. C'est le signe de la vitesse du front arrière qui détermine le caractère de l'instabilité. D'après Chomaz (1992).
\includegraphics[width=6cm]{conv-NL}
\begin{picture}(0,0)(0,0) \put( -4, 16){\makebox(0,0)[l]{$x$}} \put(-160, 74... ...ais\} quad exists v text\{~t.q.~\} A(x-vt) rightarrow infty $\}\} \end{picture}

\includegraphics[width=6cm]{abs-NL}
\begin{picture}(0,0)(0,0) \put( -4, 16){\makebox(0,0)[l]{$x$}} \put(-160, 74... ...l]\{$ A(x-vt) rightarrow infty quad forall x, quad forall v $\}\} \end{picture}


Pour un système supercritique, un état linéairement stable est non-linéairement stable et réciproquement. Par contre, Couairon et Chomaz (1999) ont montré que ce même système peut être non-linéairement absolument instable avant d'être linéairement absolument instable : la vitesse du front arrière est en effet supérieure où égale à la vitesse de groupe (travaux de Dee et Langer (1983), van Saarloos (1988)). Dans notre cas expérimental, nous n'avons pas un accès direct à cette distinction au niveau des vitesses car il nous est impossible de mesurer la vitesse du front arrière lors de l'envahissement de la cellule par la structure.


Cependant, Couairon (1997), Couairon et Chomaz (1999) ont montré sur l'équation $ {\mathbb{C}}$GL avec onde unique que l'apparition d'un mode global non-linéaire était accompagnée d'un comportement critique bien défini pour la taille de la source.


En définissant la taille de la source d'onde comme la distance entre le coeur de la source -- le bord de la cellule dans notre cas -- et la position où l'amplitude de l'onde émise vaut la moitié de sa valeur à saturation, Couairon et Chomaz ont prédit deux lois d'échelle différentes. Lorsque le seuil non-linéaire d'instabilité globale coincide avec le seuil linéaire d'instabilité absolue, la vitesse du front est alors sélectionnée linéairement (i.e., suivant le critère de Dee et Langer (1983), van Saarloos (1988)), et la taille de la source varie comme $ (\epsilon-\epsilon_{a})^{-1/2}$. Au contraire, lorsque la transition est non-linéaire, i.e., que le seuil d'instabilité globale $ \epsilon_{\text g}$ est plus bas que le seuil linéaire $ \epsilon_{\text a}$, alors la taille de la source varie en $ \ln(\epsilon-\epsilon_{\text g})$.


Comme il nous est difficile de mesurer directement la taille de la source pour les états près du seuil, nous assimilerons cette grandeur au taux de croissance spatial $ \xi_{\text s}$ de l'amplitude au niveau de la source. A première vue (Fig. [*]), le comportement critique en $ (\epsilon-\epsilon_{\text{exp}})^{-1}$ de cette grandeur ne correspond à aucun des cas linéaire ou non-linéaire répertoriés. Néanmoins, cette loi en $ (\epsilon-\epsilon_{\text{exp}})^{-1}$ que nous obtenons ne semble pas être valable très près du seuil : nous avons réalisé trois expériences pour $ \Delta T=3,66$ K, et chacune nous a donné la même valeur de $ \xi_{\text s}$, qui s'éloigne de l'ajustement linéaire bien au delà de nos barres d'erreur expérimentales. En observant différemment nos résultats (Fig. [*]), nous pouvons remarquer que la loi en puissance -1/2 (sélection linéaire) s'applique très près du seuil car elle décrit mieux les variations très rapides au départ, mais son domaine de validité est très réduit ( $ 0,18 < \epsilon < 0,21$). La loi logarithmique (sélection non linéaire) donne quand à elle une bien meilleure représentation des points expérimentaux car elle répond à ces deux critères.

Figure: Ajustement de la loi $ \xi_{\text s} (\Delta T)$ par une loi logarithmique (à gauche). Les trois différentes possibilités d'ajustement sont superposées aux données expérimentales à droite (loi linéaire, en racine carrée et logarithmique).
\includegraphics[width=8cm]{rec-xiln} \includegraphics[width=8cm]{rec-xial}


Gondret et al. (1999) ont observé une telle transition non-linéaire entre instabilité convective et absolue, associée à une divergence logarithmique de la taille de la zone de croissance. Mais le système alors étudié -- instabilité de Kelvin-Helmotz -- est un système ouvert et aucun mode de bord n'est observé en aval.


Pour étayer la discussion, remarquons que notre définition de $ \xi_{\text s}$ est légèrement différente de celle de Couairon et Chomaz (1999) qui utilisent à la place la taille de la source définie comme sa « largeur à mi-hauteur ». Si l'on note $ \xi_{1/2}$ la taille de la source et $ A_0$ l'amplitude en $ y=0$, $ A_{\text s}$ l'amplitude à saturation et $ \xi_{\text s}$ le taux de croissance spatial au voisinage de la source, alors en supposant que la variation de l'amplitude entre $ y=0$ et $ y=\xi_{1/2}$ est uniquement due à la variation exponentielle (ce qui peut ne plus être vrai au delà de $ \xi_{1/2}$ mais reste très raisonnable en dessous : cf Fig. [*]), nous pouvons écrire3.6 :

$\displaystyle A(y=\xi_{1/2}) = \displaystyle \frac{A_{\text s}}{2} \qquad \text{avec} \quad A(y)=A_0 \exp(y/\xi_{\text s}) $

$\displaystyle \Rightarrow \displaystyle \frac{\xi_{1/2}}{\xi_{\text s}} = \ln \left(\frac{A_s}{A_0} \right) - \ln 2 $

Figure: Illustration d'une croissance exponentielle au niveau de la source et saturant loin de la source. L'inclusion est en échelle logarithmique ; on y voit la définition de $ \xi_{\text s}$ comme la pente de la droite. La grandeur $ \xi_{1/2}$ est quant à elle définie comme le point d'amplitude $ A_{\text{sat}}/2$. L'ajustement logarithmique s'avère être valide pour $ y \in [0,\xi_{1/2}]$.
\includegraphics[width=8cm]{croiss}

Si nous supposons que le rapport $ A_{\text s}/A_0$ est fixé -- ce qui est le cas si l'on considère un coefficient de réflexion entre deux ondes contra-propagatives comme dans la section suivante -- alors nous trouvons que $ \xi_{\text s}$ et $ \xi_{1/2}$ sont proportionnels : nous pouvons donc comparer nos mesures ( $ \xi_{\text s}$) aux prédictions théoriques ($ \xi_{1/2}$) car les deux ont le même comportement critique. Si nous supposons au contraire que le rapport $ A_{\text s}/A_0$ n'est pas fixé, mais que c'est plutôt l'amplitude au bord amont $ A_0$ qui est constante (égale au niveau de bruit), nous écrivons alors :

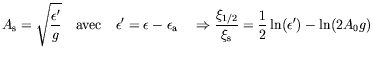
$\displaystyle A_{\text s} = \sqrt{\frac{\epsilon'}{g}} \quad \text{avec} \quad ... ... \frac{\xi_{1/2}}{\xi_{\text s}} = \frac{1}{2} \ln(\epsilon') - \ln(2 A_0 g) $

Deux régimes se dégagent donc. Le premier correspond à $ \epsilon \rightarrow 0$ ; le lien entre $ \xi_{1/2}$ et $ \xi_{\text s}$ fait alors intervenir $ \epsilon'$ et la comparaison entre théorie et expérience est non triviale. Le second régime correspond à de plus forts $ \epsilon$ pour lesquels la valeur de $ \ln(\epsilon)$ est négligeable devant $ \ln(\epsilon')$ ; nous retrouvons alors dans ce cas le même comportement critique pour $ \xi_{1/2}$ et $ \xi_{\text s}$. Vue la très faible valeur de l'amplitude aux bords, i.e. du niveau de bruit ( $ A_0 g \simeq 1$ % typiquement), le premier régime est quasiment impossible à observer.


En conclusion, nous pouvons affirmer que dans tous les cas les deux grandeurs $ \xi_{\text s}$ et $ \xi_{1/2}$ ont le même comportement critique. Nous déduisons alors de la dépendance logarithmique de $ \xi_{\text s}$ en $ \epsilon-\epsilon_{\text a}$ que la transition observée est non-linéaire.

next up previous contents
suivant: 3.1.4.3 Coefficients de réflexion monter: 3.1.4 Discussion précédent: 3.1.4.1 Formalisme convectif/absolu pour   Table des matières
Nicolas Garnier - Thèse de doctorat