



suivant: 3.1.4.2 Transition linéaire ou
monter: 3.1.4 Discussion
précédent: 3.1.4 Discussion
Table des matières
Comme nous l'avons vu en § ![[*]](crossref.png) sur le cas modèle
de l'équation
sur le cas modèle
de l'équation
 GL, l'attente de la transition convectif/absolu joue
le rôle de retardateur de l'instabilité dans le cas de la
géométrie finie aux conditions limites non périodiques. Le
décalage
GL, l'attente de la transition convectif/absolu joue
le rôle de retardateur de l'instabilité dans le cas de la
géométrie finie aux conditions limites non périodiques. Le
décalage
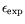 du seuil expérimental dans le
rectangle peut ainsi être expliqué de façon naturelle. La
figure
du seuil expérimental dans le
rectangle peut ainsi être expliqué de façon naturelle. La
figure ![[*]](crossref.png) représente ainsi l'évolution de
l'amplitude maximale obtenue par des simulations numériques
directes3.4 de l'équation de
représente ainsi l'évolution de
l'amplitude maximale obtenue par des simulations numériques
directes3.4 de l'équation de
 GL dans les
deux cas d'une géométrie périodique et d'une géométrie de
boîte finie.
GL dans les
deux cas d'une géométrie périodique et d'une géométrie de
boîte finie.
Figure:
Amplitude maximale
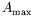 obtenue après une expérience
numérique (intégration de l'équation de Ginzburg-Landau adimensionnée
pour
obtenue après une expérience
numérique (intégration de l'équation de Ginzburg-Landau adimensionnée
pour 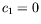 ,
, 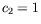 et
et
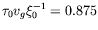 )
dans une boîte de taille
)
dans une boîte de taille 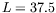 . Le cas de conditions aux limites
périodiques est repéré par l'indice
. Le cas de conditions aux limites
périodiques est repéré par l'indice 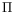 et le cas de conditions
de Dirichlet (boîte finie) par l'indice
et le cas de conditions
de Dirichlet (boîte finie) par l'indice ![$ [0,L]$](img776.png) . Dans le cas périodique,
l'amplitude est homogène dans la cellule et l'on a exactement
. Dans le cas périodique,
l'amplitude est homogène dans la cellule et l'on a exactement
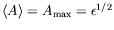 . Dans le cas de la boîte
finie, le seuil est décalé à la valeur
. Dans le cas de la boîte
finie, le seuil est décalé à la valeur
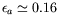 prédite par la formule (
prédite par la formule (![[*]](crossref.png) ) pour les valeurs choisies
des coefficients.
) pour les valeurs choisies
des coefficients.
|
|
Le mode global (![[*]](crossref.png) ) qui apparaît alors possède
une enveloppe spatiale bien particulière dont nous observons toutes
les caractéristiques qualitatives : annulation (au niveau de bruit
près) de l'amplitude aux bords3.5, asymétrie amont/aval due à la
propagation des ondes, croissance exponentielle de l'amplitude et valeur
maximale réalisée par conséquent en aval.
) qui apparaît alors possède
une enveloppe spatiale bien particulière dont nous observons toutes
les caractéristiques qualitatives : annulation (au niveau de bruit
près) de l'amplitude aux bords3.5, asymétrie amont/aval due à la
propagation des ondes, croissance exponentielle de l'amplitude et valeur
maximale réalisée par conséquent en aval.
Le comportement critique (puissance 1/2) de l'amplitude maximale
-- mesurée sur le mode de bord -- est donc le comportement critique
du mode global (![[*]](crossref.png) ) qui apparaît comme on l'a vu
en §
) qui apparaît comme on l'a vu
en § ![[*]](crossref.png) de façon supercritique.
de façon supercritique.
Nous pouvons alors utiliser les différentes relations définies par
l'équation (![[*]](crossref.png) ) (page
) (page ![[*]](crossref.png) ) pour
obtenir des relations entre différents coefficients des termes
linéaires de l'équation d'amplitude modélisant notre système
expérimental.
) pour
obtenir des relations entre différents coefficients des termes
linéaires de l'équation d'amplitude modélisant notre système
expérimental.




suivant: 3.1.4.2 Transition linéaire ou
monter: 3.1.4 Discussion
précédent: 3.1.4 Discussion
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) sur le cas modèle
de l'équation
sur le cas modèle
de l'équation
![[*]](crossref.png) représente ainsi l'évolution de
l'amplitude maximale obtenue par des simulations numériques
directes3.4 de l'équation de
représente ainsi l'évolution de
l'amplitude maximale obtenue par des simulations numériques
directes3.4 de l'équation de
![[*]](crossref.png) ) qui apparaît alors possède
une enveloppe spatiale bien particulière dont nous observons toutes
les caractéristiques qualitatives : annulation (au niveau de bruit
près) de l'amplitude aux bords3.5, asymétrie amont/aval due à la
propagation des ondes, croissance exponentielle de l'amplitude et valeur
maximale réalisée par conséquent en aval.
) qui apparaît alors possède
une enveloppe spatiale bien particulière dont nous observons toutes
les caractéristiques qualitatives : annulation (au niveau de bruit
près) de l'amplitude aux bords3.5, asymétrie amont/aval due à la
propagation des ondes, croissance exponentielle de l'amplitude et valeur
maximale réalisée par conséquent en aval.
![[*]](crossref.png) ) qui apparaît comme on l'a vu
en §
) qui apparaît comme on l'a vu
en § ![[*]](crossref.png) de façon supercritique.
de façon supercritique.
![[*]](crossref.png) ) (page
) (page ![[*]](crossref.png) ) pour
obtenir des relations entre différents coefficients des termes
linéaires de l'équation d'amplitude modélisant notre système
expérimental.
) pour
obtenir des relations entre différents coefficients des termes
linéaires de l'équation d'amplitude modélisant notre système
expérimental.