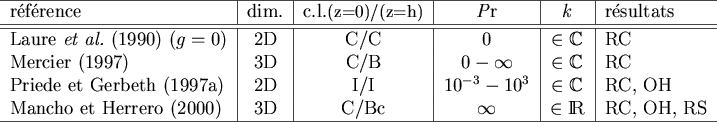suivant: 1.3.3.2 Instabilité en rouleaux
monter: 1.3.3 Instabilités stationnaires
précédent: 1.3.3 Instabilités stationnaires
Table des matières
Outre les ondes hydrothermales, l'écoulement de base se révèle
instable vis-à-vis de modulations stationnaires de vecteur d'onde
colinéaire au gradient de température appliqué. Ces modulations,
vues sur la variable vitesse, se superposent à l'écoulement de base
pour donner un écoulement structuré en rouleaux stationnaires
co-rotatifs d'axe perpendiculaire au gradient de température.
Strani et al. (1983) ont observé numériquement ces rouleaux et
Laure et al. (1990) ont donné les valeurs critiques associées à leur
apparition. Comme l'ont montré Mercier et Normand (2000), ces rouleaux doivent
être vus comme le développement spatial des perturbations dues à
la présence de bords dans la direction du gradient de température ;
un taux de croissance spatial est ainsi attaché à cette
structuration de l'écoulement. Le
tableau ![[*]](crossref.png) résume les études
théoriques ayant révélé la présence de rouleaux corotatifs
grâce à la prise en compte du confinement dans la direction du
gradient de la boîte étudiée. Le
tableau
résume les études
théoriques ayant révélé la présence de rouleaux corotatifs
grâce à la prise en compte du confinement dans la direction du
gradient de la boîte étudiée. Le
tableau ![[*]](crossref.png) présente quant à lui les
principales études numériques de l'écoulement de base et de sa
structuration. Toutes confirment le résultat suivant
de Mercier et Normand (2000), Mercier (1997) : les rouleaux apparaissent du côté
froid pour les petits nombres de Prandtl (
présente quant à lui les
principales études numériques de l'écoulement de base et de sa
structuration. Toutes confirment le résultat suivant
de Mercier et Normand (2000), Mercier (1997) : les rouleaux apparaissent du côté
froid pour les petits nombres de Prandtl (
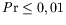 ), du côté
chaud pour les grands nombres de Prandtl (
), du côté
chaud pour les grands nombres de Prandtl (
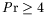 ) et des deux
côtés pour les nombres de Prandtl intermédiaires.
) et des deux
côtés pour les nombres de Prandtl intermédiaires.
Figure:
Résumé des études théoriques des écoulements thermocapillaires
en géométrie confinée dans la direction horizontale du gradient.
La colonne « dim. » indique la dimensionnalité des perturbations étudiées.
Les conditions aux limites sont abrégées : C : conducteur, I : isolant,
B : loi de Newton et nombre de Biot avec profil de température conductif
dans l'air, Bc : loi de Newton avec profil de température constant dans l'air.
La colonne 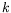 indique si le nombre d'onde est pris complexe (analyse de
stabilité spatiale) ou non. Les résultats sont notés RC : rouleaux
corotatifs, OH : ondes hydrothermales, RS : rouleaux stationnaires longitudinaux.
indique si le nombre d'onde est pris complexe (analyse de
stabilité spatiale) ou non. Les résultats sont notés RC : rouleaux
corotatifs, OH : ondes hydrothermales, RS : rouleaux stationnaires longitudinaux.
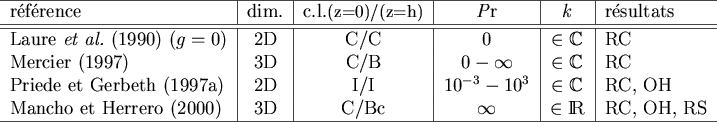 |
Notons dès à présent l'analogie formelle de notre problème avec
celui dit de la « cavité entraînée » étudié par
Bye (1966) où une contrainte mécanique1.4 est appliquée à la surface libre d'un liquide contenu dans
une cavité identique aux nôtres, et dans une moindre mesure avec le
problème de Taylor-Dean. En effet, dans ces trois cas, le profil de
vitesse est identique : il s'agit d'un profil de Couette-Poiseuille dont
les mécanismes de déstabilisation peuvent être retrouvés dans
chacun des systèmes.
Ces rouleaux ont été observés expérimentalement pour les grands
nombres de Prandtl. En géométrie rectangulaire
« unidimensionelle » Garcimartín et al. (1997) les ont vus dans une
cellule de rapport d'aspect horizontal et de hauteur appropriés
(
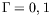 ,
, 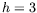 mm) ; il en est de même pour Villers et Platten (1992)
et De Saedeleer et al. (1996). Ces derniers ont mesuré précisement
l'amortissement spatial de la structure, en parfait accord avec les
prédictions de Mercier et Normand (2000). Les rouleaux corotatifs ont été
rapportés en géométrie rectangulaire étendue par
Riley et Neitzel (1998), Mukolobwiez (1998) et Pelacho et Burguete (1999).
Schwabe et al. (1992) les ont observés en géométrie cylindrique ; nous
les avons étudié en détail -- avec la visualisation de grande
qualité nécessaire -- en géométrie cylindrique
bidimensionnelle et nous rapportons des résultats quantitatifs dans le
chapitre
mm) ; il en est de même pour Villers et Platten (1992)
et De Saedeleer et al. (1996). Ces derniers ont mesuré précisement
l'amortissement spatial de la structure, en parfait accord avec les
prédictions de Mercier et Normand (2000). Les rouleaux corotatifs ont été
rapportés en géométrie rectangulaire étendue par
Riley et Neitzel (1998), Mukolobwiez (1998) et Pelacho et Burguete (1999).
Schwabe et al. (1992) les ont observés en géométrie cylindrique ; nous
les avons étudié en détail -- avec la visualisation de grande
qualité nécessaire -- en géométrie cylindrique
bidimensionnelle et nous rapportons des résultats quantitatifs dans le
chapitre ![[*]](crossref.png) (§
(§ ![[*]](crossref.png) ).
).




suivant: 1.3.3.2 Instabilité en rouleaux
monter: 1.3.3 Instabilités stationnaires
précédent: 1.3.3 Instabilités stationnaires
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) résume les études
théoriques ayant révélé la présence de rouleaux corotatifs
grâce à la prise en compte du confinement dans la direction du
gradient de la boîte étudiée. Le
tableau
résume les études
théoriques ayant révélé la présence de rouleaux corotatifs
grâce à la prise en compte du confinement dans la direction du
gradient de la boîte étudiée. Le
tableau ![[*]](crossref.png) présente quant à lui les
principales études numériques de l'écoulement de base et de sa
structuration. Toutes confirment le résultat suivant
de Mercier et Normand (2000), Mercier (1997) : les rouleaux apparaissent du côté
froid pour les petits nombres de Prandtl (
présente quant à lui les
principales études numériques de l'écoulement de base et de sa
structuration. Toutes confirment le résultat suivant
de Mercier et Normand (2000), Mercier (1997) : les rouleaux apparaissent du côté
froid pour les petits nombres de Prandtl (