



suivant: 1.3.4.2 Effet de la
monter: 1.3.4 Instabilités en ondes
précédent: 1.3.4 Instabilités en ondes
Table des matières
Les ondes apparaissent avec une fréquence et un nombre d'onde finis.
La prise en compte des effets thermogravitaires et/ou de déflections
de la surface peut, dans les cas limites où ceux-ci sont importants,
conduire à d'autres modes d'instabilités de fréquences
différentes. Pour la fréquence des ondes hydrothermales, un assez
bon accord existe entre les résultats expérimentaux dans l'huile de
silicone (Garcimartín et al. (1997), Pelacho et Burguete (1999), Mukolobwiez (1998)) et les
prédictions théoriques (Smith et Davis (1983a), Mercier (1997)). De
nombreux résultats expérimentaux sur les ondes hydrothermales dans
l'huile que nous utilisons, dans des géométries rectangulaires
étendues, sont présentés et discutés dans l'article de
Burguete et al. (2000) ; nous donnons dans le tableau de la
figure ![[*]](crossref.png) un aperçu des différentes
expériences rapportées.
un aperçu des différentes
expériences rapportées.
Figure:
Résumé des études théoriques de la stabilité temporelle
des écoulements thermocapillaires en géométrie infinie rectangulaire.
Le gradient de température est toujours horizontal.
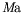 signifie la prise en compte de la tension de surface,
signifie la prise en compte de la tension de surface,
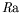 la prise
en compte de la thermogravité et
la prise
en compte de la thermogravité et 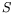 la prise en compte des déflections
de surface. La colonne « dim. » indique la dimensionnalité des
perturbations considérées. Les conditions limites thermiques sont
notées ainsi : I : isolant, C : conducteur, B : nombre de Biot.
Les modes observés sont notés ainsi :
OH : ondes hydrothermales, MH : modes hydrodynamiques (
la prise en compte des déflections
de surface. La colonne « dim. » indique la dimensionnalité des
perturbations considérées. Les conditions limites thermiques sont
notées ainsi : I : isolant, C : conducteur, B : nombre de Biot.
Les modes observés sont notés ainsi :
OH : ondes hydrothermales, MH : modes hydrodynamiques (
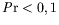 ),
OS : ondes de surface, RS : rouleaux stationnaires
longitudinaux.
),
OS : ondes de surface, RS : rouleaux stationnaires
longitudinaux.
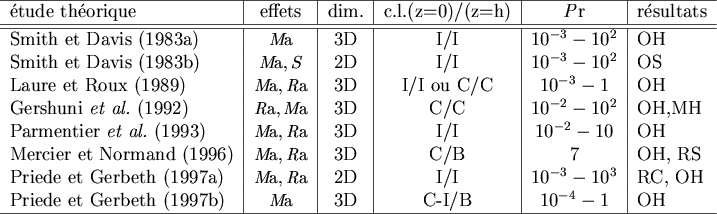 |
Figure:
Résumé des études numériques des écoulements thermocapillaires.
La colonne « dim. » indique la dimensionnalité de la simulation numérique.
Les conditions limites thermiques sont notées I pour isolant, C pour conducteur
et Bc pour l'utilisation de la loi de Newton avec profil de température
constant dans l'air.
RC : rouleaux corotatifs, O : oscillations temporelles issues de la
déstabilisation du premier rouleau ou de la couche limite.
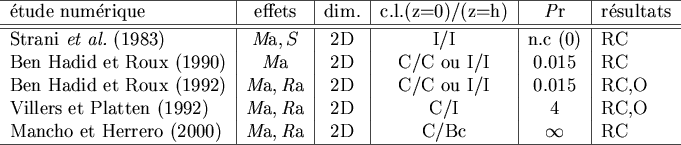 |
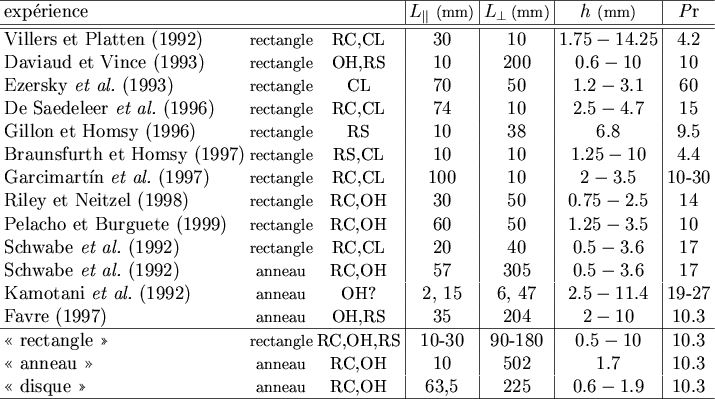
Figure:
Synthèse des études expérimentales imposant un gradient
horizontal de température à une mince couche de fluide avec
surface libre.
Les structures observées sont abrégées ainsi :
RC : rouleaux corotatifs structurant l'écoulement de base,
OH : ondes hydrothermales bien caractérisées se propageant du froid
vers le chaud,
RS : rouleaux stationnaires d'axe colinéaire au gradient de température,
CL : instabilité de couche limite ou du premier rouleau du côté chaud
produisant des ondes voyageant du chaud vers le froid.
 |
Les ondes apparaissent avec un angle de propagation 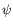 entre le
gradient de température et leur vecteur d'onde ; nous détaillons un
peu plus cette notion d'angle en §
entre le
gradient de température et leur vecteur d'onde ; nous détaillons un
peu plus cette notion d'angle en § ![[*]](crossref.png) . La
figure
. La
figure ![[*]](crossref.png) fixe les idées en géométrie
rectangulaire. Avec les notations précédentes en géométrie
cylindrique, nous avons :
fixe les idées en géométrie
rectangulaire. Avec les notations précédentes en géométrie
cylindrique, nous avons :
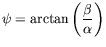
car
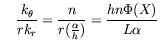
Figure:
Schéma illustrant la définition de l'angle de
propagation 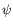 des ondes.
des ondes.
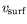 : vitesse du fluide
en surface, du chaud vers le froid.
Le vecteur d'onde
: vitesse du fluide
en surface, du chaud vers le froid.
Le vecteur d'onde 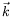 a pour composantes
a pour composantes
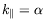 selon
selon
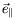 et
et
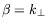 selon
selon
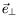 .
.
|
|
Smith et Davis (1983a), Smith (1986) ont montré une dépendance de
cet angle en fonction du nombre de Prandtl (uniquement). Ainsi, pour les
petits nombres de Prandtl, les ondes sont attendues avec un vecteur
d'onde presque colinéaire au gradient de température ; plus le
nombre de Prandtl augmente et plus l'angle augmente jusqu'à ce que le
vecteur d'onde soit presque perpendiculaire au gradient. Les
expériences ont confirmé l'ordre de grandeur mais seule une faible
gamme de nombre de Prandtl a été parcourue. Parmentier et al. (1993),
Mercier (1997) ont eux montré une dépendance de 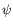 vis-a-vis
de
vis-a-vis
de 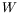 . Pour les plus faibles valeurs de
. Pour les plus faibles valeurs de 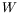 , i.e. les plus grandes
valeurs de
, i.e. les plus grandes
valeurs de 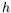 , l'angle
, l'angle 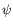 est nul; pour les plus grandes valeurs de
est nul; pour les plus grandes valeurs de
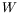 , i.e. les plus faibles valeurs de
, i.e. les plus faibles valeurs de 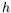 , l'angle est fini et proche de
, l'angle est fini et proche de
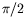 .
.




suivant: 1.3.4.2 Effet de la
monter: 1.3.4 Instabilités en ondes
précédent: 1.3.4 Instabilités en ondes
Table des matières
Nicolas Garnier - Thèse de doctorat

![[*]](crossref.png) un aperçu des différentes
expériences rapportées.
un aperçu des différentes
expériences rapportées.



![]() entre le
gradient de température et leur vecteur d'onde ; nous détaillons un
peu plus cette notion d'angle en §
entre le
gradient de température et leur vecteur d'onde ; nous détaillons un
peu plus cette notion d'angle en § ![[*]](crossref.png) . La
figure
. La
figure ![[*]](crossref.png) fixe les idées en géométrie
rectangulaire. Avec les notations précédentes en géométrie
cylindrique, nous avons :
fixe les idées en géométrie
rectangulaire. Avec les notations précédentes en géométrie
cylindrique, nous avons :
![\begin{picture}(180,160)(-175,0)
\put(-175, 0){\includegraphics[width=6cm]{angl...
...0)[b]{$T_{+} > T_{-}$}}
\put( -90, 10){\makebox(0,0)[t]{$T_{-}$}}
\end{picture}](img280.png)