



suivant: 5.1.4 A propos des
monter: 5.1 Transition 1D /
précédent: 5.1.2.2 Source d'onde
Table des matières
5.1.3 Petit bilan et convention adoptée
- A grande hauteur, les ondes hydrothermales sont des ondes planes
« unidimensionelles » émises par une source de codimension 1. Nous
les qualifions d'ondes hydrothermales de type 1 : OH1.
- A petite hauteur, les ondes observées sont cylindriques près
de la source, puis confinées en ondes planes par la géométrie.
Ces ondes « bidimensionnelles » sont émises par une source de
codimension 2. Nous les qualifions d'ondes hydrothermales de type 2 :
OH2.
Rappelons ici la notion d'angle local 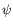 entre le gradient de
température appliqué
entre le gradient de
température appliqué
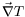 et le vecteur d'onde de la
structure
et le vecteur d'onde de la
structure 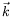 (cf Fig.
(cf Fig. ![[*]](crossref.png) ). Cette définition est
naturelle et peut être utilisée sur un cliché ombroscopique pour
obtenir une valeur de
). Cette définition est
naturelle et peut être utilisée sur un cliché ombroscopique pour
obtenir une valeur de 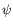 à
à 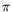 près. En ce sens,
près. En ce sens, 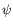 peut
être baptisée « angle statique ». Nous l'appellons abusivement
« angle de propagation » car c'est aussi l'angle entre
peut
être baptisée « angle statique ». Nous l'appellons abusivement
« angle de propagation » car c'est aussi l'angle entre
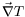 et la vitesse de phase
et la vitesse de phase
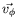 -- cette dernière étant
colinéaire à
-- cette dernière étant
colinéaire à 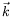 . Néanmoins, nous savons
(chapitre
. Néanmoins, nous savons
(chapitre ![[*]](crossref.png) par exemple) que la vitesse de groupe est
souvent plus pertinente que la vitesse de phase ; il serait donc plus
judicieux d'introduire l'angle de propagation comme l'angle entre le
gradient de température et la vitesse de groupe. Pour autant, nous
nous contenterons de
par exemple) que la vitesse de groupe est
souvent plus pertinente que la vitesse de phase ; il serait donc plus
judicieux d'introduire l'angle de propagation comme l'angle entre le
gradient de température et la vitesse de groupe. Pour autant, nous
nous contenterons de 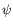 car les théories de stabilité linéaire
l'utilisent (
car les théories de stabilité linéaire
l'utilisent (
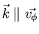 , et cf
§
, et cf
§ ![[*]](crossref.png) ) et de plus
) et de plus 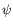 est directement mesurable sur
des clichés, et il est donc plus facile de l'interpréter en termes
géométriques. Rappelons :
est directement mesurable sur
des clichés, et il est donc plus facile de l'interpréter en termes
géométriques. Rappelons :

Figure:
Schéma illustrant la définition « naturelle » de l'angle de
propagation 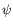 des ondes.
des ondes.
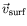 : vitesse du fluide
en surface, du chaud vers le froid.
: vitesse du fluide
en surface, du chaud vers le froid.
|
|




suivant: 5.1.4 A propos des
monter: 5.1 Transition 1D /
précédent: 5.1.2.2 Source d'onde
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) ). Cette définition est
naturelle et peut être utilisée sur un cliché ombroscopique pour
obtenir une valeur de
). Cette définition est
naturelle et peut être utilisée sur un cliché ombroscopique pour
obtenir une valeur de ![[*]](crossref.png) par exemple) que la vitesse de groupe est
souvent plus pertinente que la vitesse de phase ; il serait donc plus
judicieux d'introduire l'angle de propagation comme l'angle entre le
gradient de température et la vitesse de groupe. Pour autant, nous
nous contenterons de
par exemple) que la vitesse de groupe est
souvent plus pertinente que la vitesse de phase ; il serait donc plus
judicieux d'introduire l'angle de propagation comme l'angle entre le
gradient de température et la vitesse de groupe. Pour autant, nous
nous contenterons de ![[*]](crossref.png) ) et de plus
) et de plus 
![\begin{picture}(180,160)(-175,0)
\put(-175, 0){\includegraphics[width=6cm]{angl...
...0)[b]{$T_{+} > T_{-}$}}
\put( -90, 10){\makebox(0,0)[t]{$T_{-}$}}
\end{picture}](img280.png)