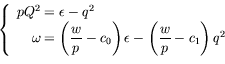![[*]](crossref.png) ) de nombre
d'onde
) de nombre
d'onde
Mais comme nous l'avons noté, nous observons expérimentalement une
dissymétrie
![]() et une fermeture « par le dessus » ;
aucun de ces deux effets n'est présent dans le cas de l'équation de
Ginzburg-Landau. Nous introduisons donc des termes supplémentaires
d'ordre supérieur (4 et 5 en
et une fermeture « par le dessus » ;
aucun de ces deux effets n'est présent dans le cas de l'équation de
Ginzburg-Landau. Nous introduisons donc des termes supplémentaires
d'ordre supérieur (4 et 5 en
![]() dans notre cas au lieu
de l'ordre 3 habituel de
dans notre cas au lieu
de l'ordre 3 habituel de
![]() GL) dans l'équation d'amplitude.
Introduire ces termes permet d'avoir au seuil une équation de
GL) dans l'équation d'amplitude.
Introduire ces termes permet d'avoir au seuil une équation de
![]() GL
classique qui se déforme progressivement au fur et à mesure que
GL
classique qui se déforme progressivement au fur et à mesure que
![]() est augmenté. Nous proposons ainsi :
est augmenté. Nous proposons ainsi :
 |
(B.1) |
Parmi tous les termes d'ordre 4 possibles en ![]() et
et
![]() --
-- ![]() ,
, ![]() ,
,
![]() ,
,
![]() --, seuls
--, seuls ![]() et
et ![]() ont
été retenus car les autres peuvent être écrits comme des
combinaisons linéaires de ces deux-là.
ont
été retenus car les autres peuvent être écrits comme des
combinaisons linéaires de ces deux-là. ![]() et les autres
termes en
et les autres
termes en
![]() d'ordre plus élevé ne sont pas étudiés
car ils se signalent par une dépendance prononcée des amplitudes et
fréquences vis-à-vis du nombre d'onde, ce qui n'est pas observé
dans les expériences. D'autres termes d'ordre 4 en
d'ordre plus élevé ne sont pas étudiés
car ils se signalent par une dépendance prononcée des amplitudes et
fréquences vis-à-vis du nombre d'onde, ce qui n'est pas observé
dans les expériences. D'autres termes d'ordre 4 en ![]() sont
envisageables mais immédiatement éliminés pour des raisons de
non-résonnance (
sont
envisageables mais immédiatement éliminés pour des raisons de
non-résonnance (![]() ,
, ![]() ,
, ![]() ).
).
Parmi tous les termes d'ordre 5 (beaucoup plus nombreux), seul un terme
(
![]() ) a été conservé car sa signature dans la
pseudo-relation de dispersion ne fait pas intervenir des puissance de
) a été conservé car sa signature dans la
pseudo-relation de dispersion ne fait pas intervenir des puissance de
![]() trop élevées et reste donc proche des résultats
expérimentaux. Remarquons toutefois l'existence d'autres candidats
possibles comme
trop élevées et reste donc proche des résultats
expérimentaux. Remarquons toutefois l'existence d'autres candidats
possibles comme ![]() , qui a la même signature dans la relation
de dispersion et qui ne rend pas le système instable vis-à-vis des
gradients de phase élevés.
, qui a la même signature dans la relation
de dispersion et qui ne rend pas le système instable vis-à-vis des
gradients de phase élevés.
Remarque : La vitesse de groupe ![]() a été éliminée car
nous sommes en géométrie périodique. Cette équation ne décrit
qu'une seule onde et la symétrie
a été éliminée car
nous sommes en géométrie périodique. Cette équation ne décrit
qu'une seule onde et la symétrie
![]() , associée à
l'inversion
, associée à
l'inversion
![]() n'est de toute façon pas
respectée par une seule équation
n'est de toute façon pas
respectée par une seule équation
![]() GL. La présence de termes
autorisés à briser la symétrie
GL. La présence de termes
autorisés à briser la symétrie
![]() , donc la symétrie
, donc la symétrie
![]() est justifiée par le même argument.
est justifiée par le même argument.
Remarque : Nous pouvons interpréter les termes que nous avons
rajoutés, non comme des termes d'ordre supérieur en ![]() , mais
comme les termes suivants du développement de la partie non-linéaire
de l'équation en puissance de l'écart au nombre d'onde critique
(développement en
, mais
comme les termes suivants du développement de la partie non-linéaire
de l'équation en puissance de l'écart au nombre d'onde critique
(développement en ![]() ). C'est alors l'approche de
Eckhaus et Iooss (1989).
). C'est alors l'approche de
Eckhaus et Iooss (1989).
Convention : Pour des raisons de clarté, nous
adimensionnalisons l'équation (![[*]](crossref.png) ) comme
exposé en
) comme
exposé en ![[*]](crossref.png) et nous posons dans toute la suite :
et nous posons dans toute la suite :
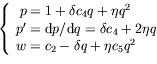
![[*]](crossref.png) ), nous
avons les relations de dispersion (dimensionnées) suivantes :
), nous
avons les relations de dispersion (dimensionnées) suivantes :