



suivant: B.2 Modélisation
monter: B. Instabilité d'Eckhaus supercritique
précédent: B. Instabilité d'Eckhaus supercritique
Table des matières
La figure ![[*]](crossref.png) est un diagramme des phases obervées
expérimentalement et reproduites dans le plan
est un diagramme des phases obervées
expérimentalement et reproduites dans le plan
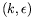 . Chaque
petit cercle (
. Chaque
petit cercle (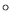 ) correspond à un état stable, i.e. d'amplitude
et de gradients de phase parfaitement homogènes. Au contraire, les
croix (
) correspond à un état stable, i.e. d'amplitude
et de gradients de phase parfaitement homogènes. Au contraire, les
croix (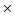 ) correspondent à des états instables où une
modulation de phase pousse jusqu'à conduire à une ou plusieurs
dislocations spatiotemporelles ; l'amplitude s'annule alors, la phase
subit une discontinuité de
) correspondent à des états instables où une
modulation de phase pousse jusqu'à conduire à une ou plusieurs
dislocations spatiotemporelles ; l'amplitude s'annule alors, la phase
subit une discontinuité de 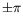 et le système change de nombre
d'onde. De même, les croix (
et le système change de nombre
d'onde. De même, les croix (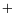 ) correspondent à des états
instables où le système relaxe vers une absence d'ondes. Un
quatrième type d'état est représenté par des petites étoiles
(
) correspondent à des états
instables où le système relaxe vers une absence d'ondes. Un
quatrième type d'état est représenté par des petites étoiles
(
 ) ; il s'agit d'états instables vis-à-vis de modulations
de phase qui saturent non-linéairement : ces états ne conduisent pas
à une dislocation spatio-temporelle, comme l'on montré
Mukolobwiez et al. (1998).
) ; il s'agit d'états instables vis-à-vis de modulations
de phase qui saturent non-linéairement : ces états ne conduisent pas
à une dislocation spatio-temporelle, comme l'on montré
Mukolobwiez et al. (1998).
Figure:
Etats stables et instables dans le plan
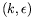 pour
l'anneau avec
pour
l'anneau avec 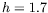 mm. Cette figure constitue une tranche de
ballon de stabilité.
La courbe continue représente la limite de stabilité marginale
déduite des résultats expérimentaux
(cf annexe
mm. Cette figure constitue une tranche de
ballon de stabilité.
La courbe continue représente la limite de stabilité marginale
déduite des résultats expérimentaux
(cf annexe ![[*]](crossref.png) ).
).
![\begin{picture}(0,0)(0,0)
\put(248,328){\makebox(0,0)[l]{\'etat stable}}
\put(...
...et dislocation}}
\put(248,277){\makebox(0,0)[l]{absence d'ondes}}
\end{picture}](img1198.png) |
Ce diagramme de stabilité nous montre clairement le processus de
sélection du nombre d'onde lorsque  est augmenté ou
diminué. Nous observons effectivement :
est augmenté ou
diminué. Nous observons effectivement :
- une fermeture « par le dessus » de la zone de stabilité
qui donne à la zone stable l'allure d'une chaussette.
- une très nette asymétrie entre les nombres d'ondes
 (
(
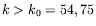 ) et les nombres d'ondes
) et les nombres d'ondes 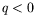 (
(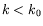 ).
).




suivant: B.2 Modélisation
monter: B. Instabilité d'Eckhaus supercritique
précédent: B. Instabilité d'Eckhaus supercritique
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) est un diagramme des phases obervées
expérimentalement et reproduites dans le plan
est un diagramme des phases obervées
expérimentalement et reproduites dans le plan
![]() est augmenté ou
diminué. Nous observons effectivement :
est augmenté ou
diminué. Nous observons effectivement :