



suivant: 3.2.3.2 b. Etats absolument
monter: 3.2.3 Cas de l'expérience
précédent: 3.2.3 Cas de l'expérience
Table des matières
Lorsque  est augmenté à partir du seuil primaire des ondes
tel qu'étudié en §
est augmenté à partir du seuil primaire des ondes
tel qu'étudié en § ![[*]](crossref.png) , une onde majoritaire envahit
progressivement toute la cellule en éliminant l'onde inverse.
S'installe alors un régime où l'onde majoritaire (que nous prendrons
toujours être une onde droite) atteint son amplitude à saturation
presque partout dans la cellule. La fréquence et le nombre d'onde sont
uniformes et ce dernier est à peu près constant, et vaut environ
, une onde majoritaire envahit
progressivement toute la cellule en éliminant l'onde inverse.
S'installe alors un régime où l'onde majoritaire (que nous prendrons
toujours être une onde droite) atteint son amplitude à saturation
presque partout dans la cellule. La fréquence et le nombre d'onde sont
uniformes et ce dernier est à peu près constant, et vaut environ
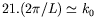 ce qui signifie que 21 longueurs d'onde sont
présentes dans la boîte ; nous appellerons ainsi l'onde
correspondante le « mode 21 ». Jusqu'à
ce qui signifie que 21 longueurs d'onde sont
présentes dans la boîte ; nous appellerons ainsi l'onde
correspondante le « mode 21 ». Jusqu'à
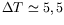 K, ce
mode est parfaitement homogène et stable. La
figure
K, ce
mode est parfaitement homogène et stable. La
figure ![[*]](crossref.png) représente en fonction de
représente en fonction de  l'évolution du nombre d'onde local dans la cellule, ainsi que de la
fréquence.
l'évolution du nombre d'onde local dans la cellule, ainsi que de la
fréquence.
Au delà de 5,5 K environ, l'instabilité d'Eckhaus survient dans la
cellule rectangulaire tout comme dans la cellule annulaire. Nous
observons ainsi une instabilité de la phase du mode 21 ; cette
instabilité est signée par l'apparition de modulations conduisant
éventuellement à des dislocations qui permettent à un nouveau mode
de s'installer. Ce nouveau mode est appellé mode 17 (mode dont le
nombre d'onde vaut environ
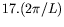 ). Nous avons pu mesurer le
nombre d'onde local et la fréquence locale dans chacune des zones 21
et 17 ; la figure
). Nous avons pu mesurer le
nombre d'onde local et la fréquence locale dans chacune des zones 21
et 17 ; la figure ![[*]](crossref.png) révèle ainsi la présence
de l'instabilité secondaire par le dédoublement des courbes de
nombre d'onde et de fréquence. A partir de diagrammes spatio-temporels
de fréquence ou de nombre d'onde local(e) instantané(e), nous
pouvons mesurer le nombre d'onde et la fréquence des modulations dans
le régime instable d'Eckhaus ; ces valeurs sont ainsi reproduites sur
la figure
révèle ainsi la présence
de l'instabilité secondaire par le dédoublement des courbes de
nombre d'onde et de fréquence. A partir de diagrammes spatio-temporels
de fréquence ou de nombre d'onde local(e) instantané(e), nous
pouvons mesurer le nombre d'onde et la fréquence des modulations dans
le régime instable d'Eckhaus ; ces valeurs sont ainsi reproduites sur
la figure ![[*]](crossref.png) . Nous pouvons remarquer que le
nombre d'onde de la modulation est égal à la différence des
nombres d'onde du mode 21 et du mode 17 ; il en est de même pour la
fréquence des modulations. Il est aussi possible de mesurer un taux de
croissance temporel de la modulation
. Nous pouvons remarquer que le
nombre d'onde de la modulation est égal à la différence des
nombres d'onde du mode 21 et du mode 17 ; il en est de même pour la
fréquence des modulations. Il est aussi possible de mesurer un taux de
croissance temporel de la modulation 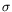 , lors des régimes
transitoires par exemple ; nous définirons aussi plus loin un taux de
croissance spatial.
, lors des régimes
transitoires par exemple ; nous définirons aussi plus loin un taux de
croissance spatial.
La vitesse de groupe étant finie (cf Fig. ![[*]](crossref.png) ), cette
instabilité est a priori convective au seuil, et devient
éventuellement absolue au delà d'un second seuil, situé plus haut.
Le petit schéma ci-dessous situe les principaux régimes
d'instabilité d'Eckhaus du mode 21 :
), cette
instabilité est a priori convective au seuil, et devient
éventuellement absolue au delà d'un second seuil, situé plus haut.
Le petit schéma ci-dessous situe les principaux régimes
d'instabilité d'Eckhaus du mode 21 :
![\begin{picture}(400,50)(-100,-20)
\linethickness{1pt}
\put(-100, 0){\vector(...
...ebox(0,0)[b]{stable ?}}
\put( -50, 10){\makebox(0,0)[b]{stable}}
\end{picture}](img833.png)
Pour des raisons de clarté, nous exposerons nos résultats en
commençant par les plus hautes valeurs de  , pour
lesquelles l'instabilité d'Eckhaus est absolue, et nous descendrons
progressivement les valeurs de
, pour
lesquelles l'instabilité d'Eckhaus est absolue, et nous descendrons
progressivement les valeurs de  .
.
Figure:
Evolution du nombre d'onde (à gauche) et de la fréquence (à droite)
dans le rectangle lorsque l'on s'éloigne du seuil d'apparition des ondes
et que survient l'instabilité d'Eckhaus. Le segment sur le graphe de
gauche repère la zone de  étudiée en §
étudiée en § ![[*]](crossref.png) au voisinage du seuil primaire (la figure
au voisinage du seuil primaire (la figure ![[*]](crossref.png) est ainsi un détail dans cette zone).
Les deux branches au delà de
est ainsi un détail dans cette zone).
Les deux branches au delà de
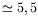 K
signalent l'instabilité modulationnelle d'Eckhaus (voir texte).
Les carrés (
K
signalent l'instabilité modulationnelle d'Eckhaus (voir texte).
Les carrés ( ) et les ronds (
) et les ronds (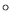 ) correspondent
respectivement aux modes 21 et 17.
) correspondent
respectivement aux modes 21 et 17.
![\begin{picture}
% latex2html id marker 7740
(0,0)(0,0)
\put( 68, 68){\makebox(0,0)[t]{\S~\ref{sec:abs:rect}}}
\end{picture}](img836.png) |
Figure:
Evolution de la vitesse de phase
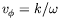 (à gauche) et
de la vitesse de groupe (à droite, mesurée comme vitesse de propagation de
perturbations) dans le rectangle en fonction de
(à gauche) et
de la vitesse de groupe (à droite, mesurée comme vitesse de propagation de
perturbations) dans le rectangle en fonction de  .
Les carrés (
.
Les carrés ( ) et les ronds (
) et les ronds (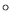 ) correspondent respectivement
au modes 21 et 17. Le premier point du graphe de la vitesse de groupe,
pour
) correspondent respectivement
au modes 21 et 17. Le premier point du graphe de la vitesse de groupe,
pour
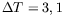 K, correspond à la valeur au seuil dans l'anneau.
K, correspond à la valeur au seuil dans l'anneau.
|
|
Figure:
Evolution du nombre d'onde (à gauche) et de la fréquence (à droite)
de la modulation de phase dans le rectangle en fonction de  lorsque des états instables d'Eckhaus sont observés.
lorsque des états instables d'Eckhaus sont observés.
|
|
A titre indicatif, le rapport des fréquences des modes 21 et 17 est
reproduit sur la figure ![[*]](crossref.png) . Ce rapport semble à peu
près constant et sa valeur (1,13 = 113/100) est assez loin d'une
fraction non-réductible simple. Nous en déduisons qu'il n'y a pas
d'accrochage entre les deux modes 21 et 17.
. Ce rapport semble à peu
près constant et sa valeur (1,13 = 113/100) est assez loin d'une
fraction non-réductible simple. Nous en déduisons qu'il n'y a pas
d'accrochage entre les deux modes 21 et 17.
Figure:
Evolution du rapport des fréquences du mode 21
et du mode 17 dans la zone de températures où le mode 21 est instable d'Eckhaus
et où le mode 17 est stable d'Eckhaus.
|
|
Figure:
Représentations schématiques de l'amplitude d'une modulation d'Eckhaus
sur un état convectivement instable et absolument instable en géométrie
finie ou semi-infinie. Tout comme sur la figure ![[*]](crossref.png) ,
c'est le signe de la vitesse du front
arrière qui détermine le caractère de l'instabilité.
L'instabilité n'est pas saturée non-linéairement, mais éclate en
un trou d'amplitude associé à un saut de phase. Le front avant est
par conséquent
esclave du front arrière (cf. le taux de croissance spatial est
constant). Ces schémas sont une reprise épurée des résultats
expérimentaux.
,
c'est le signe de la vitesse du front
arrière qui détermine le caractère de l'instabilité.
L'instabilité n'est pas saturée non-linéairement, mais éclate en
un trou d'amplitude associé à un saut de phase. Le front avant est
par conséquent
esclave du front arrière (cf. le taux de croissance spatial est
constant). Ces schémas sont une reprise épurée des résultats
expérimentaux.
|
|




suivant: 3.2.3.2 b. Etats absolument
monter: 3.2.3 Cas de l'expérience
précédent: 3.2.3 Cas de l'expérience
Table des matières
Nicolas Garnier - Thèse de doctorat
![[*]](crossref.png) révèle ainsi la présence
de l'instabilité secondaire par le dédoublement des courbes de
nombre d'onde et de fréquence. A partir de diagrammes spatio-temporels
de fréquence ou de nombre d'onde local(e) instantané(e), nous
pouvons mesurer le nombre d'onde et la fréquence des modulations dans
le régime instable d'Eckhaus ; ces valeurs sont ainsi reproduites sur
la figure
révèle ainsi la présence
de l'instabilité secondaire par le dédoublement des courbes de
nombre d'onde et de fréquence. A partir de diagrammes spatio-temporels
de fréquence ou de nombre d'onde local(e) instantané(e), nous
pouvons mesurer le nombre d'onde et la fréquence des modulations dans
le régime instable d'Eckhaus ; ces valeurs sont ainsi reproduites sur
la figure ![[*]](crossref.png) . Nous pouvons remarquer que le
nombre d'onde de la modulation est égal à la différence des
nombres d'onde du mode 21 et du mode 17 ; il en est de même pour la
fréquence des modulations. Il est aussi possible de mesurer un taux de
croissance temporel de la modulation
. Nous pouvons remarquer que le
nombre d'onde de la modulation est égal à la différence des
nombres d'onde du mode 21 et du mode 17 ; il en est de même pour la
fréquence des modulations. Il est aussi possible de mesurer un taux de
croissance temporel de la modulation ![\includegraphics[width=8cm]{rec-k-2}](img834.png)
![\includegraphics[width=8cm]{rec-f-2}](img835.png)
![\includegraphics[width=8cm]{rec-vph}](img839.png)
![\includegraphics[width=8cm]{rec-vg}](img840.png)
![\includegraphics[width=8cm]{k-mod}](img843.png)
![\includegraphics[width=8cm]{f-mod}](img844.png)
![\includegraphics[width=8cm]{f21-f17}](img845.png)
![\includegraphics[width=6cm]{conv-ec}](img846.png)
![\begin{picture}(0,0)(0,0)
\put( -4, 18){\makebox(0,0)[l]{$x$}}
\put(-157, 88...
...ais\} quad exists v text\{~t.q.~\} A(x-vt) rightarrow infty $\}\}
\end{picture}](img847.png)
![\includegraphics[width=6cm]{abs-ec}](img848.png)
![\begin{picture}(0,0)(0,0)
\put( -4, 18){\makebox(0,0)[l]{$x$}}
\put(-157, 88...
...l]\{$ A(x-vt) rightarrow infty quad forall x, quad forall v $\}\}
\end{picture}](img849.png)