| Nombre de Grashoff : |
|
=
|
=
|
||
| Nombre de Bond dynamique : |
|
=
|
=
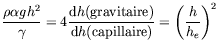 |
||
| ou son inverse : | =
|
=
|
|||
| Nombre de Reynolds gravitaire : |
|
=
|
=
|
||
| Nombre de Reynolds capillaire : |
|
=
|
=
|
| Nombre de Grashoff : |
|
=
|
=
|
||
| Nombre de Bond dynamique : |
|
=
|
=
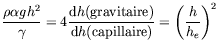 |
||
| ou son inverse : | =
|
=
|
|||
| Nombre de Reynolds gravitaire : |
|
=
|
=
|
||
| Nombre de Reynolds capillaire : |
|
=
|
=
|
Application numérique : Par définition, nous avons ![]() si
si
![]() . Pour l'huile utilisée (cf §
. Pour l'huile utilisée (cf § ![[*]](crossref.png) ), nous
avons
), nous
avons
![]() pour
pour ![]() mm,
mm,
![]() pour
pour ![]() mm et
mm et
![]() pour
pour ![]() mm. Ainsi, dans tous les cas envisagés
ici, les effets thermogravitaires sont négligeables devant les effets
thermocapillaires, du moins pour l'écoulement de base.
mm. Ainsi, dans tous les cas envisagés
ici, les effets thermogravitaires sont négligeables devant les effets
thermocapillaires, du moins pour l'écoulement de base.
Remarque : Les nombres de Reynolds gravitaire et capillaire
peuvent être directement obtenus comme des nombres de Reynolds
![]() en considérant comme vitesse
en considérant comme vitesse ![]() la vitesse caractéristique
d'un écoulement gravitaire ou capillaire. Par exemple, dans le cas
thermocapillaire, la vitesse caractéristique (d'une particule fluide
de la surface libre) peut être écrite en équilibrant la force de
dissipation visqueuse agissant sur un volume
la vitesse caractéristique
d'un écoulement gravitaire ou capillaire. Par exemple, dans le cas
thermocapillaire, la vitesse caractéristique (d'une particule fluide
de la surface libre) peut être écrite en équilibrant la force de
dissipation visqueuse agissant sur un volume ![]() (
(
![]() )
à la force due à la variation de la tension de surface et
s'appliquant sur une surface
)
à la force due à la variation de la tension de surface et
s'appliquant sur une surface ![]() (
(
![]() ) :
) :
Application numérique : Dans la cellule rectangulaire 1D
(![]() mm,
mm, ![]() mm), pour
mm), pour
![]() K il vient
K il vient
![]() = 90 mm/s. Dans la cellule disque 2D
(
= 90 mm/s. Dans la cellule disque 2D
(![]() mm,
mm, ![]() mm), pour
mm), pour
![]() K, il vient
K, il vient
![]() = 48 mm/s. Nous pouvons en déduire l'ordre de
grandeur du temps nécessaire au fluide pour parcourir exactement un
rouleau complet de l'écoulement de base, i.e. une « période » :
0,3 s pour le rectangle et 2,7 s pour le disque. Ces valeurs sont
surestimées car la vitesse du fluide n'est qu'au plus égale à sa
vitesse en surface.
= 48 mm/s. Nous pouvons en déduire l'ordre de
grandeur du temps nécessaire au fluide pour parcourir exactement un
rouleau complet de l'écoulement de base, i.e. une « période » :
0,3 s pour le rectangle et 2,7 s pour le disque. Ces valeurs sont
surestimées car la vitesse du fluide n'est qu'au plus égale à sa
vitesse en surface.