



suivant: 1.1.2.0.6 Cas limite des
monter: 1.1.2 Réduction de la
précédent: 1.1.2.0.4 Autres nombres sans
Table des matières
La pression capillaire
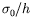 peut être comparée aux pressions
hydrostatique et hydrodynamique pour donner respectivement le nombre de
Bond et le nombre capillaire. En comparant les forces de tension de
surface aux forces de frottement visqueux, nous obtenons le nombre de
« tension de surface » :
peut être comparée aux pressions
hydrostatique et hydrodynamique pour donner respectivement le nombre de
Bond et le nombre capillaire. En comparant les forces de tension de
surface aux forces de frottement visqueux, nous obtenons le nombre de
« tension de surface » :
| Nombre de Bond : |
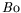 |
| =
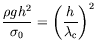 (
(
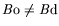 !) !) |
| |
|
| |
| Nombre capillaire : |
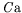 |
| =
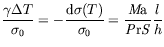 |
| |
|
| |
| Nombre de « tension de surface » : |
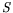 |
| =
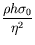 |
| |
|
| |
| Nombre de crispation : |
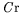 |
| =
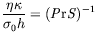 |
| |
|
| |
Ces nombres font intervenir la tension de surface, et non plus seulement
sa dérivée. Ils permettent de mesurer l'importance des déflections
de la surface libre. Ainsi, la surface est plate si
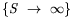 , i.e.
, i.e.
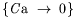 ; nous nous
plaçons dans ce cas pour tous nos calculs de l'écoulement de base.
; nous nous
plaçons dans ce cas pour tous nos calculs de l'écoulement de base.




suivant: 1.1.2.0.6 Cas limite des
monter: 1.1.2 Réduction de la
précédent: 1.1.2.0.4 Autres nombres sans
Table des matières
Nicolas Garnier - Thèse de doctorat
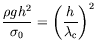 (
(
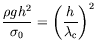 (
(
![]() , i.e.
, i.e.
![]() ; nous nous
plaçons dans ce cas pour tous nos calculs de l'écoulement de base.
; nous nous
plaçons dans ce cas pour tous nos calculs de l'écoulement de base.