



suivant: 1.2 Calcul de l'écoulement
monter: 1.1.2 Réduction de la
précédent: 1.1.2.0.7 Remarque et bilan
Table des matières
Pour compléter notre inventaire de nombres sans dimension dans le
cadre d'une approche hydrodynamique, il est nécessaire d'introduire
les dimensions spatiales normalisées par la hauteur 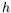 ; cela
définit les deux rapports d'aspects géométriques horizontaux :
; cela
définit les deux rapports d'aspects géométriques horizontaux :
| direction du gradient : |
|
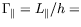 |
 |
| direction orthogonale au gradient : |
|
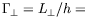 |
 |
Il est ensuite possible de combiner ces deux quantités pour obtenir :
qui mesure le rapport d'aspect du système horizontal où
l'on s'est affranchi de la dimension verticale.
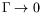 est ainsi la signature d'un système unidimensionnel dans la direction
perpendiculaire au gradient -- la cellule rectangulaire étroite est
dans ce cas --, et
est ainsi la signature d'un système unidimensionnel dans la direction
perpendiculaire au gradient -- la cellule rectangulaire étroite est
dans ce cas --, et
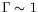 la signature d'un système
bidimensionnel -- la cellule cylindrique en forme de disque, baptisée
« LOTUS », est dans ce cas.
la signature d'un système
bidimensionnel -- la cellule cylindrique en forme de disque, baptisée
« LOTUS », est dans ce cas.
Nicolas Garnier - Thèse de doctorat



